Corrente Alternata Sinusoidale II
La Corrente Alternata
Reattanza e Impedenza. Bipoli RLC serie. Risonanza
Sintesi. Analizzando il comportamento in regime sinusoidale del resistore, dell'induttore e del condensatore ideali, si introducono i concetti di reattanza e impedenza. Si studiano quindi i bipoli ottenuti collegando in serie questi componenti anche in funzione della frequenza. Viene preso quindi in considerazione il fenomeno della risonanza serie o di tensione.
Convenzioni tipografiche. Usiamo lettere puntate, ad esempio \(\small \dot{V},\, \dot{I},\, \dot{Z}\) per rappresentare fasori e operatori complessi. La stessa notazione rappresenta anche i corrispondenti numeri complessi ( es. \(\small \dot{Z} = R +j\,X\)). Riserviamo però la notazione standard per i vettori rotanti (es \(\small \vec{I}, \vec{V}\)).
Lettere non puntate indicano i moduli di grandezze complesse o vettoriali (es. \(\small Z = \sqrt{R^2 + X^2}\)).
Per l'unità immaginaria, in luogo della lettera \(\small i = \sqrt{-1}\) come in matematica, utilizzeremo qui la lettera \(\small j = \sqrt{-1}\). Quando desideriamo mettere in evidenza la dipendenza funzionale da altre grandezze come il tempo, usiamo lettere minuscole, cosi ad esempio: \(\small v(t) = V_M\,sin(\omega t)\).
Premessa.
Per una più completa comprensione di quanto qui esposto potrà essere utile consultare il modulo precedente di questa serie: Corrente Alternata 1: Generazione di una Tensione Sinusoidale, in cui sono presentati alcuni concetti fondamentali, tra cui un'introduzione al "metodo simbolico" e all'uso dei numeri complessi per la trattazione dei circuiti in corrente alternata sinusoidale.
1 - Circuiti elettrici in regime alternato sinusoidale
 La fem è una differenza di potenziale (ddp), misurata in volt, cioè un'energia potenziale per unità di carica: \(\small 1\, volt = \dfrac{1\,joule}{1\,coulomb}\).
Il dispositivo che produce questa differenza di potenziale è chiamato
generatore di tensione. Esso, inserito in un circuito
elettrico di
cui fanno parte anche dispositivi utilizzatori dell'energia elettrica,
provocherà il movimento di
La fem è una differenza di potenziale (ddp), misurata in volt, cioè un'energia potenziale per unità di carica: \(\small 1\, volt = \dfrac{1\,joule}{1\,coulomb}\).
Il dispositivo che produce questa differenza di potenziale è chiamato
generatore di tensione. Esso, inserito in un circuito
elettrico di
cui fanno parte anche dispositivi utilizzatori dell'energia elettrica,
provocherà il movimento di
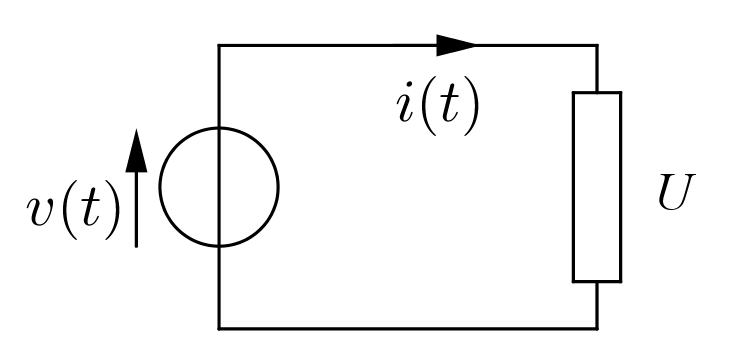
Figura 1 - Circuito con generatore e utilizzatore
\(\qquad \qquad \qquad i(t)= \dfrac{\Delta q(t)}{\Delta t} \qquad \qquad i(t)= \dfrac{d\, q(t)}{d\, t}\)
la prima espressione intesa come rapporto tra variazioni finite, la seconda, conoscendo il calcolo differenziale, come derivata della carica elettrica rispetto al tempo.
Il movimento di cariche è dovuto al campo elettrico legato alla tensione impressa \(\small v(t)\) e, nel caso di fem alternata sinusoidale, è costituito da un'oscillazione armonica dell'insieme degli elettroni di conduzione presenti nel reticolo cristallino.
Questo studio è limitato alle correnti e tensioni stazionarie: si tratta di correnti e tensioni sinusoidali in cui le caratteristiche della sinusoide quali frequenza, ampiezza e fase non variano nel tempo. In questo caso diciamo che il circuito elettrico funziona in regime alternato sinusoidale.
1.1 - Sinusoidi e numeri complessi
Prima di continuare, non sarà inutile ricordare che le sinusoidi possono convenientemente essere rappresentate da numeri complessi.
Figura 2 - Vettori e numeri complessi
Una sinusoide \(\small y(t)\) di pulsazione \(\small \omega \) potrà allora essere rappresentata dal numero complesso \(\small a+jb\) se: \(\small y(t) = \sqrt{2} \,\sqrt{a^2 + b^2} sin(\omega t + \beta)\), con \(\small \beta = arctan \left( \dfrac{b}{a}\right)\).
Fissato \(\small \omega\) avremo quindi la corrispondenza biunivoca:
\( \qquad \qquad a + j\,b\;\Longleftrightarrow\; \sqrt{2} \,\sqrt{a^2 + b^2}\, sin(\omega t + \beta) \qquad \beta = arctan \left( \dfrac{b}{a}\right)\).
analogamente per la forma esponenziale:
\( \qquad \qquad \sqrt{a^2 + b^2}\, e^{j\,\beta}\;\Longleftrightarrow\; \sqrt{2} \,\sqrt{a^2 + b^2}\, sin(\omega t + \beta) \).
o la forma polare nella notazione di Steinmetz:
\( \qquad \qquad \sqrt{a^2 + b^2}\, \angle \beta\;\Longleftrightarrow\; \sqrt{2} \,\sqrt{a^2 + b^2}\, sin(\omega t + \beta) \).
La presenza del fattore \(\small \sqrt{2}\) è dovuta al fatto che con i moduli dei fasori si rappresentano i valori efficaci piuttosto che le ampiezze.
Queste corrispondenze stanno alla base del metodo simbolico, o analisi fasoriale, per il calcolo dei circuiti elettrici in corrente alternata sinusoidale.
Tuttavia, come verrà chiarito in seguito, non tutti i numeri complessi vengono interpretati come sinusoidi. Alcuni assumono il ruolo di operatori agenti sulle sinusoidi stesse.
1.2 - Impedenza
È particolarmente importante poter stabilire una relazione tra tensione impressa dal generatore \(\small v(t)\) e corrente \(\small i(t)\) nel circuito. Vedremo che questa relazione esiste, ma non è esprimibile in maniera semplice, come avviene in corrente continua con la legge di Ohm.Per ora scriviamola in questa forma:
(1) \( \qquad \qquad \qquad \qquad v(t) = Z\, i(t) \qquad \qquad Z =\, ? \).
La grandezza \(\small Z\) di cui dobbiamo comprendere natura e struttura matematica, viene detta impedenza, e può essere considerarata come un operatore che trasforma una sinusoide in un'altra: \(\small Z : i(t) \rightarrow v(t)\)

Figura 3 - L'operatore impedenza Z trasforma una corrente sinusoidale in una tensione sinusoidale. L'unità di misura di Z è l'ohm \(\small \Omega\).
Dato allora un circuito elettrico semplice, come quello di figura 1, con un generatore di fem alternata sinusoidale \(\small v(t)= V_M\,sin(\omega t)\) e un utilizzatore di energia elettrica U, ci proponiamo di descrivere la corrente attraverso una opportuna funzione sinusoidale \(\small i(t)= I_M\,sin(\omega t + \theta)\), della quale si deve determinare l'ampiezza \(\small I_M\) e la fase \(\small \theta\), e di determinare la grandezza \(\small Z\) attraverso la quale \(\small v(t)\) e \(\small i(t)\) sono in relazione.
Poichè l'impedenza \(\small Z\) è certamente legata alla natura e alle caratteristiche elettriche dell'utilizzatore, cominciamo l'analisi con lo studio di tre casi limite:
a) utilizzatore (carico) puramente resistivo
b) utilizzatore (carico) puramente induttivo
c) utilizzatore (carico) puramente capacitivo
Il comportamento di ogni utilizzatore reale ovviamente presenta aspetti propri di tutti e tre i casi elencati, in maggior o minor misura. Non è possibile infatti prescindere dalla presenza di una resistenza anche per un solenoide o un condensatore, così come non si possono eliminare completamente gli effetti induttivi e/o capacitivi per un carico resistivo. Evidentemente per una bobina saranno prevalenti gli effetti induttivi, per un condensatore quelli capacitivi, ecc.
Lo studio dei casi limite è importante perchè consente un'analisi semplificata e una comprensione più agevole. Il caso reale può poi venir trattato come sovrapposizione delle situazioni ideali studiate.
2 - Utilizzatore puramente resistivo
 L'utilizzatore
equivale ad un resistore
(1) di resistenza R ideale
(privo di effetti induttivi e capacitivi) a cui viene applicata la
tensione alternata sinusoidale (supponiamo nulla la fase della tensione, per semplicità):
L'utilizzatore
equivale ad un resistore
(1) di resistenza R ideale
(privo di effetti induttivi e capacitivi) a cui viene applicata la
tensione alternata sinusoidale (supponiamo nulla la fase della tensione, per semplicità):(2) \( \qquad \qquad \qquad \qquad v(t) = V_M\,sin(\omega t) \).
Un resistore non è in grado di accumulare energia. Essa viene dissipata totalmente, istante per istante, sotto forma di calore per effetto Joule. Il dispositivo è quindi energeticamente passivo: semplicemente converte tutta l'energia elettrica assorbita in calore.
Ai capi del resistore si forma una caduta di tensione che presenta polarità istantanea positiva sul terminale di entrata della corrente convenzionale.
Le polarità positive istantanee sono indicate dalla punta delle frecce che rappresentano le differenze di potenziale (ddp).
La corrente \(\small i(t)\) segue esattamente l'andamento della tensione \(\small v(t)\) che qui coincide con la caduta di tensione \(\small v_R(t)\) sul resistore secondo la relazione lineare:
(3) \( \qquad \qquad \qquad \qquad v_R(t) = R\,i(t) \).
ovvero:
(4) \( \qquad \qquad \qquad \qquad v_R(t) = R\,I_M\,sin(\omega t) \).
da cui, considerando la (2), deduciamo che l'ampiezza della tensione deve essere:
(5) \( \qquad \qquad \qquad \qquad V_M = V_{R_M} = R\, I_M \).
In termini di valori efficaci:
(6) \( \qquad \qquad \qquad \qquad V_R = \dfrac{V_{RM}}{\sqrt{2}} \qquad \qquad I = \dfrac{I_M}{\sqrt{2}}\).
essa può essere scritta come:
(7) \( \qquad \qquad \qquad \qquad V_R = R\, I \).
Se si rappresentano le sinusoidi mediante i fasori \(\small \dot{V_R}\) e \(\small \dot{I}\), si trova che questi sono in fase, cioè l'angolo relativo che essi formano ha valore nullo. La tensione \(\small \dot{V_R}\) si ottiene moltiplicando \(\small \dot{I}\) per il numero reale \(\small R\), in questo caso \(\small Z = R\), per cui:
(8) \( \qquad \qquad \qquad \qquad \dot{V_R} = R\, \dot{I} \)
Un carico di questo tipo è detto anche puramente ohmico.
 Attività1
Attività1
2.1 - Energia e potenza
Si è detto che il resistore trasforma istantaneamente l'energia assorbita \(\small w(t)\), convertendola in calore per effetto Joule. Ciò è dovuto alla trasformazione dell'energia cinetica degli elettroni in movimento in energia di vibrazione degli atomi del reticolo cristallino e degli elettroni stessi.Per trasferire una certa quantità di energia \(\small \Delta w(t)\) si impiega un tempo \(\small \Delta t\);vi è allora in gioco una potenza \(\small p(t) = \dfrac{\Delta w(t)}{\Delta t} =v(t)\,i(t) = R\,i^2(t) \).
Questa potenza è sempre positiva dato che dipende dal quadrato della corrente. Questo significa che essa fluisce in un solo senso: dal generatore verso l'utilizzatore.
La caratteristica di questa potenza è che essa può essere "estratta" dal sistema elettrico e, almeno parzialmente, convertita in lavoro. Si può ad esempio riscaldare dell'acqua attraverso il calore generato dal resistore fino a trasformarla in vapore, che immesso in un turbina collegata ad un alternatore ne provoca la rotazione.
Una potenza di questo tipo viene detta potenza attiva.
Per approfondire i concetti di potenza attiva e reattiva:
 Potenza in corrente
alternata sinusoidale
Potenza in corrente
alternata sinusoidale
3 - Utilizzatore puramente induttivo
 Un induttore
puro può essere pensato come un
avvolgimento (o un solenoide) di N spire realizzato con
conduttore assolutamente privo di resistenza e di effetti capacitivi,
caratterizzato da un coefficiente di autoinduzione, o
induttanza, \(\small L\).
Un induttore
puro può essere pensato come un
avvolgimento (o un solenoide) di N spire realizzato con
conduttore assolutamente privo di resistenza e di effetti capacitivi,
caratterizzato da un coefficiente di autoinduzione, o
induttanza, \(\small L\).Le considerazioni seguenti si avvalgono del concetto di derivata di una funzione. Se si desidera una trattazione che non utilizzi il calcolo differenziale vedere il successivo paragrafo 3.1.
Come è noto il coefficiente di autoinduzione \(\small L\) mette in relazione il flusso magnetico \(\small \phi_c(t) \) concatenato(2) o autoflusso con la corrente che lo genera:
(9) \( \qquad \qquad \qquad \qquad \phi_c(t) = L\,i(t) \)
Dato che si tratta di un flusso variabile nel tempo, l'induttore stesso sarà sede di una fem autoindotta secondo la nota relazione:
(10) \( \qquad \qquad \qquad \qquad e(t) = -L\,\dfrac{d\,i(t)}{d\,t} \)
Se la corrente \(\small i(t)\) è sinusodale e ha forma:
(11) \( \qquad \qquad \qquad \qquad i(t) =I_M\,sin(\omega t) \)
applicando le regole di derivazione, dalla (10) si ha immediatamente:
(12) \( \qquad e(t) = -L\,\dfrac{d\,i(t)}{d\,t} = - \omega\,L\,I_M\,cos(\omega t) = \omega\,L\,I_M\,sin \left(\omega t - \dfrac{\pi}{2}\right) \)
da cui si deduce che \(\small e(t)\) è in ritardo di un quarto di periodo sulla corrente o come si usa dire: \(\small e(t)\) è in quadratura in ritardo su \(\small i(t)\).
Il prodotto \(\small \omega\,L\) della pulsazione per il coefficiente di autoinduzione viene indicato con \(\small X_L\) o semplicemente con \(\small X\) e prende il nome di reattanza induttiva:
(13) \( \qquad \qquad \qquad \qquad X_L = \omega\,L = 2\,\pi\,f\,L \)
La (13) mette anche in evidenza la dipendenza diretta di \(\small X_L\) dalla frequenza.
Dalla relazione (12) abbiamo allora:
(14) \( \qquad \qquad \qquad \qquad e(t) = X_L\,I_M\,sin \left(\omega t - \dfrac{\pi}{2}\right) \)
Ai capi dell'induttore si forma quindi una fem \(\small e(t)\) che è in ritardo di un quarto di periodo sulla corrente e avrà ampiezza:
(15) \( \qquad \qquad \qquad \qquad E_M = X_L\,I_M \)
e valore efficace:
(15') \( \qquad \qquad \qquad \qquad E = X_L\,I \qquad \qquad \qquad E= \dfrac{E_M}{\sqrt{2}}\qquad I = \dfrac{I_M}{\sqrt{2}} \)
Le (15,15') suggeriscono che anche la reattanza induttiva debba essere misurata in ohm (\(\small \Omega \)).
Tuttavia qui c'è un problema: pur dando una corretta espressione per i moduli, (15) e (15') nulla dicono sulle relazioni di fase tra le grandezze in gioco. Ciò significa che le equazioni (15, 15') non forniscono una informazione completa sul comportamento del sistema. Come risolvere allora questo problema?
 Attività 2
Attività 2
Per approfondire gli aspetti dell'autoinduzione:
 Autoinduzione in regime alternato sinusoidale
Autoinduzione in regime alternato sinusoidale
3.1 - Reattanza induttiva: una dimostrazione con i vettori rotanti
 Può essere utile e istruttivo giungere alle precedenti conclusioni ragionando sui
vettori rotanti, senza ricorrere al calcolo differenziale. È noto (v. Grandezze
elettriche sinusoidali) che sinusoidi di egual frequenza
possono essere rappresentate da vettori rotanti.
Vediamo nella
lavagna la sinusoide corrente \(\small i(t)\) e il corrispondente vettore rotante \(\small \vec{I}\)(3).
L'angolo \(\small \omega t\) ovviamente varia allo scorrere
del tempo.
Può essere utile e istruttivo giungere alle precedenti conclusioni ragionando sui
vettori rotanti, senza ricorrere al calcolo differenziale. È noto (v. Grandezze
elettriche sinusoidali) che sinusoidi di egual frequenza
possono essere rappresentate da vettori rotanti.
Vediamo nella
lavagna la sinusoide corrente \(\small i(t)\) e il corrispondente vettore rotante \(\small \vec{I}\)(3).
L'angolo \(\small \omega t\) ovviamente varia allo scorrere
del tempo.Rappresentiamo la situazione in un istante generico \(\small t \). Disegniamo ora il vettore nella posizione che occupava in un istante precedente \(\small t - \Delta t\). Tra le due posizioni successive vi è una distanza angolare \(\small \omega \Delta t\), ciò significa che il vettore corrente \(\small \vec{I}\), partendo dalla posizione \(\small \vec{I}(t - \Delta t)\), giunge in \(\small \vec{I}(t)\) dopo \(\small \Delta t\) secondi, avendo percorso un angolo \(\small \omega \Delta t\) radianti.
In questo intervallo di tempo il vettore \(\small \vec{I}(t)\) ha subito una variazione, perchè, pur non essendo cambiato il modulo, sono cambiate la direzione ed il verso. La variazione deve essere a sua volta un vettore :
(16) \( \qquad \qquad \qquad \qquad \Delta \vec{ I} = \vec{I}(t) - \vec{I}(t - \Delta t) \)
o, se si preferisce:
(17) \( \qquad \qquad \qquad \qquad \vec{I}(t) = \vec{I}(t - \Delta t) + \Delta \vec{I} \)
cioè il vettore in una certa posizione si può ottenere dal vettore in una posizione precedente sommando la variazione \(\small \Delta \vec{I}\).
In tutti questi discorsi il parametro \(\small \Delta t\) gioca un ruolo critico, nel senso che la consistenza del ragionamento e la precisione dei risultati dipendono fortemente dal suo valore.
L'intervallo di tempo \(\small \Delta t\) deve assumere valori molto piccoli, prossimi allo zero. In tal caso il modulo di \(\small \vec{I}(t)\) risulta praticamente uguale alla lunghezza dell'arco sotteso da \(\small \vec{I}(t)\) stesso e può essere calcolato, allo stesso modo della lunghezza dell'arco, come prodotto di
(18) \( \qquad \qquad \qquad \qquad \Delta I = I_M\,\omega \Delta t \)
Dalla (10), che conviene qui scrivere in forma vettoriale ( \(\small \vec{E}\) e \(\small \vec{I}\)sono i vettori rotanti rappresentativi delle sinusoidi ):
(19) \( \qquad \qquad \qquad \qquad \vec{E} = -L\, \dfrac{\Delta \vec{I}}{\Delta t} \)
possiamo ricavare il vettore \(\small \vec{E}\), che ha la stessa direzione di \(\small \Delta \vec{I}\), ma verso opposto a causa del segno meno che compare in (19). Il suo modulo, considerando la (18), risulta essere:
(20) \( \qquad \qquad \qquad \qquad E = L\, \dfrac{I_M\,\omega \Delta t}{\Delta t} = \omega\,L\,I_M \)
Notiamo che mentre \(\small \Delta I\) dipende dall'intervallo temporale \(\small \Delta t\), non è così per \(\small E\), come risulta dalla (20).
Il vettore \(\small \vec{E}\) può essere applicato nell'origine mediante una traslazione (operazione che lascia invariato il vettore, dato che viene spostato parallelamente a se stesso senza deformazione), in modo da rappresentare più agevolmente la sinusoide \(\small e(t)\).
Osserviamo ora che diminuendo il valore di \(\small \Delta t\), il vettore \(\small \vec{E}\) tende a disporsi perpendicolarmente rispetto al vettore (rotante) \(\small \vec{I}\). Ciò spiega il fatto che la fem autoindotta risulta essere in ritardo di \(\small \dfrac{\pi}{2} \) sulla corrente.
La tensione impressa \(\small \vec{V}\) dal generatore non può che essere uguale ed opposta ad \(\small \vec{E}\) perchè altrimenti non sarebbe possibile la circolazione di una corrente stazionaria.
Anche in questo caso è opportuno traslare il vettore tensione applicandolo nell'origine.
La tensione impressa è quindi in quadratura in anticipo sulla corrente (oppure la corrente è in quadratura in ritardo sulla tensione impressa). Viene anche messo in evidenza l'angolo di sfasamento reciproco \(\small \varphi\) di cui si può verificare la dipendenza da \(\small \Delta t\), notando che al diminuire di quest'ultimo si approssima sempre meglio un angolo retto.
3.2 - Energia magnetica, potenza e fem autoindotta
Per quale motivo si crea la fem (10) e perchè essa è in quadratura in ritardo rispetto alla corrente?La corrente che scorre nell'induttore crea un campo magnetico cui corrisponde un'energia \(\small w\) immagazzinata nel volume di spazio occupato dal campo:
(21) \( \qquad \qquad \qquad \qquad w(t) = \dfrac{1}{2}\,L\,i^2(t) \)
questa è la risposta alle due domande precedenti. L'induttore è un dispositivo che accumula e rilascia l'energia immagazzinata sotto forma di campo magnetico. L'energia è accumulata quando la fem \(\small e(t)\) si oppone alla corrente con l'induttore che si comporta da utilizzatore. Viene invece restituita al generatore quando \(\small e(t)\) e corrente sono concordi e l'induttore si comporta da generatore.
La potenza necessaria per trasferire l'energia (21) non può essere estratta dal sistema generatore-induttore. Con essa non si può quindi eseguire lavoro su qualche sistema esterno. Una potenza con tali caratteristiche è detta potenza reattiva.
In questo gioco di scambi enrgetici e di potenza la tensione impressa dal generatore elettrico \(\small v(t)\) deve essere sempre uguale ed opposta alla \( \small e(t)\) per poter consentire la circolazione di una corrente stazionaria senza alcuna dissipazione di potenza, data ad esempio dalla (11):
(22) \( \qquad v(t) = -e(t) = L \dfrac{d\,i(t)}{d\,t}= \omega\,L\,I_M\,cos(\omega t) = \omega\,L\,I_M\,sin \left(\omega t +\dfrac{\pi}{2}\right) \)
da cui:
(23) \( \qquad \qquad \qquad \qquad v(t) = X_L\,I_M\,sin \left(\omega t +\dfrac{\pi}{2}\right) \)
e quindi:
(24) \( \qquad \qquad \qquad \qquad V_M = X_L\,I_M \)
oppure considerando i valori efficaci \(\small V = \dfrac{V_M}{\sqrt{2}}\) e \(\small I = \dfrac{I_M}{\sqrt{2}}\):
(25) \( \qquad \qquad \qquad \qquad V = X_L\,I \)
Potremmo anche qui dire che \(\small Z = X_L\), ma, sebbene vera dal punto di vista dei moduli, tale relazione non sarebbe del tutto precisa dal momento che le relazioni (24) o (25), valide per le ampiezze o i loro valori efficaci, non dicono alcunché rispetto alle fasi reciproche delle sinusoidi, cioè, ad esempio, rispetto al fatto che la sinusoide \(\small i(t)\) deve essere in ritardo di fase pari a \(\small \dfrac{\pi}{2}\) sulla tensione \(\small v(t)\).
Per tale ragione non è sufficiente considerare \(\small X_L\) come un semplice numero reale.
3.3 - La reattanza induttiva è un numero immaginario
 Dunque le
relazioni tra tensione impressa, fem autoindotta e
corrente non possono limitarsi a coinvolgere ampiezze o valori
efficaci, dato che si deve in qualche modo tener conto degli
sfasamenti tra grandezze.
Dunque le
relazioni tra tensione impressa, fem autoindotta e
corrente non possono limitarsi a coinvolgere ampiezze o valori
efficaci, dato che si deve in qualche modo tener conto degli
sfasamenti tra grandezze. Consideriamo ancora una volta la situazione che si presenta in un circuito puramente induttivo.
Osservando le due sinusoidi abbiamo che:
\( \qquad \qquad \qquad v(t) = V_M\,sin(\omega t) \qquad \qquad i(t) = I_M\,sin \left(\omega t - \dfrac{\pi}{2}\right)\)
Ad esse, come sappiamo, corrispondono i numeri complessi in forma polare:
\( \qquad \qquad \qquad \dot{V} = \dfrac{V_M}{\sqrt{2}}\,\angle 0° = V\,\angle 0° \qquad \quad \dot{I} = \dfrac{I_M}{\sqrt{2}}I\,\angle -90° = I\,\angle -90°\)
o in forma algebrica:
\( \qquad \qquad \qquad \dot{V} = V+j\,0 \qquad \qquad \qquad \dot{I} = 0 -j\,I\)
che rappresentano i rispettivi fasori.
Ora, se vogliamp individuare una relazione tra queste grandezze potremmo scrivere, utilizzando l'operatore impedenza:
\[ \dot{V} = \dot{Z}\, \dot{I}\] In effetti abbiamo già scritto \(\small \dot{Z}\) avendo capito che l'impedenza dovrà essere a sua volta un numero complesso, dato che la moltiplicazione per un semplice numero reale non è in grado di agire sugli angoli di fase.
In particolare, in questo caso, dovendo produrre una rotazione di fase di 90°, vedremo che l'impedenza sarà costituita da un numero immaginario puro: la reattanza complessa
\[ \dot{Z} = \dot{X_L} = j\,X_L\] Proviamo allora a scrivere la relazione cercata nei termini:
\[ \dot{V} = j\,X_L\,\dot{I} \] \[ V + j\,0 = j\,X_L (0 -j\,I) \] eseguendo il prodotto (notiamo che \(\small V + j\,0 = V\) è un numero reale (fase 0°):
\[ \dot{V} = j\,X_L (0 -j\,I) = -j^2 X_L\,I = -(-1) \omega\,L\,I\] ottenendo quindi:
\[ V + j\,0 = \omega\,L\,I + j\,0\] che è ancora un numero reale, come in effetti doveva essere.
L'operatore impedenza \(\small \dot{Z}\) applicato al fasore \(\small \dot{I}\), oltre che agire sul modulo, deve provocare una rotazione di \(\small \dfrac{\pi}{2}\), in modo che la tensione risulti in anticipo di tale angolo sulla corrente (da \(\small -\dfrac{\pi}{2}\) a \(\small 0\) nel nostro caso). Quindi \( \dot{Z}\) non può che essere un numero complesso e, nel caso particolare, un numero complesso immaginario. Ricordiamo infatti che ( Numeri Complessi, paragrafo 1.2.4) l'unità immaginaria \(\small j\) può essere interpretata come operatore di rotazione di \(\small \dfrac{\pi}{2}\) in senso antiorario. Se quindi rappresentiamo le grandezze sinusoidali come fasori, a loro volta espressi da numeri complessi ( Grandezze Elettriche Alternate Sinusoidali), la relazione cercata diventa:
(26) \( \qquad \qquad \qquad \qquad \qquad \dot{V} = j\,X_L\,\dot{I} \)
Volendo potremmo anche scrivere la relazione tra \(\small \dot{E}\) ed \(\small \dot{I}\):
(27) \( \qquad \qquad \qquad \qquad \qquad \dot{E} = -j\,X_L\,\dot{I} \)
dato che \(\small -j\) opera la rotazione opposta.
Infine elenchiamo le forme possibili per l'operatore reattanza induttiva:
forma algebrica: \( \qquad \qquad \qquad \qquad \qquad \dot{X_L} = j\,X_L \)
forma esponenziale: \( \qquad \qquad \qquad \qquad \dot{X_L} = X_L\,e^{\,j\,\small \dfrac{\pi}{2}} \)
forma polare: \( \qquad \qquad \qquad \qquad \qquad \dot{X_L} = X_L \angle 90° \)
con il modulo: \( \qquad \qquad \qquad \qquad \qquad X_L = \omega\,L = 2\,\pi\,f\,L \quad \Omega \)
4 - Utilizzatore puramente capacitivo
 Analizziamo
ora il comportamento di un utilizzatore puramente capacitivo,
che identifichiamo con un condensatore ideale.
Analizziamo
ora il comportamento di un utilizzatore puramente capacitivo,
che identifichiamo con un condensatore ideale.Il dielettrico del condensatore è sede di un campo elettrico generato dalla distribuzione di carica \(\small q(t)\) sulle armature. Essa è in relazione con la differenza di potenziale \(\small v(t)\) tra le armature stesse, attraverso la capacità C, che supponiamo costante:
(28) \( \qquad \qquad \qquad \qquad \qquad d\,q(t) = C\, d\,v(t) \)
(28') \( \qquad \qquad \qquad \qquad \qquad \Delta\,q(t) = C\, \Delta\,v(t) \)
dove abbiamo usato sia la forma differenziale (28) che quella alle differenze finite (28').
Le due formule precedenti affermano che, qualsiasi variazione di carica sulle armature si riflette proporzionalmente sulla variazione della ddp tra le armature stesse o, viceversa, che qualsiasi variazione di ddp tra le armature comporta una variazione di carica su di esse. La costante di proporzionalità è appunto la capacità C del condensatore.
Una variazione di carica comporta però la presenza di una corrente elettrica e infatti, se pensiamo di dividere la (28) per \(\small d\,t\) o la (28') per \(\small \Delta\, t\), posto che:
(29) \( \qquad \qquad \qquad \qquad \qquad i(t) = \dfrac{d\,q(t)}{d\,t} \)
(29') \( \qquad \qquad \qquad \qquad \qquad i(t) = \dfrac{\Delta\,q(t)}{\Delta\,t} \)
otteniamo l'equazione differenziale:
(30) \( \qquad \qquad \qquad \qquad \qquad i(t) = C\, \dfrac{d\,v(t)}{d\,t} \)
o alle differenze finite:
(30') \( \qquad \qquad \qquad \qquad \qquad i(t) = C\, \dfrac{\Delta\,v(t)}{\Delta\,t} \)
Se confrontiamo la (30) con la (10) possiamo constatare che dal punto di vista matematico le equazioni sono formalmente identiche (isomorfe). Solamente, tensione e corrente si scambiano di ruolo.
Ricaviamo ora la relazione tra tensione e corrente con l'ausilio del calcolo differenziale:
(31) \( \qquad \qquad \qquad \qquad \qquad v(t) = V_M\, sin (\omega t) \)
dalla (30) abbiamo che:
(32) \( \qquad i(t) = C\,V_M\, \dfrac{d\,sin(\omega t)}{d\,t} = \omega\,C\,V_M\, cos(\omega t) = \omega\,C\,V_M\,sin \left(\omega t +\dfrac{\pi}{2} \right) \)
Dalla quale notiamo subito che la sinusoide della corrente \(\small i(t)\) è in anticipo di \(\small \dfrac{\pi}{2}\) sulla sinusoide della tensione \(\small v(t)\) sulle armature del condensatore, che coincide con la tensione ai terminali del generatore (e anche con la sua fem se è un generatore ideale).
L'ampiezza della corrente è:
(33) \( \qquad \qquad \qquad \qquad \qquad I_M = \omega\,C\, V_M \)
da cui:
(34) \( \qquad \qquad \qquad \qquad \qquad V_M = \dfrac{1}{\omega\,C\,}\, I_M \)
relazione che sussiste anche tra valori efficaci:
(35) \( \qquad \qquad \qquad \qquad \qquad V = \dfrac{1}{\omega\,C}\, I \)
Porremo quindi:
(36) \( \qquad \qquad \qquad \qquad \qquad X_C = \dfrac{1}{\omega\,C} = \dfrac{1}{2\,\pi\,f\,C} \)
definendo in tal modo la reattanza capacitiva \(\small X_C\).
Da notare la proporzionalità inversa rispetto alla frequenza.
 Attività 3
Attività 3
4.1 - Reattanza capacitiva: una dimostrazione con i vettori rotanti
 Anche qui torna utile ritrovare le relazioni tra tensione
e corrente ricorrendo alle equazioni alle differenze finite e
ai vettori rotanti, sebbene, dal punto di vista matematico, si tratti
di una sostanziale ripetizione di quanto esposto in 3.1, con gli
opportuni adattamenti.
Anche qui torna utile ritrovare le relazioni tra tensione
e corrente ricorrendo alle equazioni alle differenze finite e
ai vettori rotanti, sebbene, dal punto di vista matematico, si tratti
di una sostanziale ripetizione di quanto esposto in 3.1, con gli
opportuni adattamenti.Rappresentiamo nella lavagna la sinusoide tensione \(\small v(t)\) e il corrispondente vettore rotante \(\small \vec{V}\). L'angolo \(\small \omega t\) varia allo scorrere del tempo, ma consideriamo la situazione in un istante generico \(\small t\). Disegniamo ora il vettore nella posizione che occupava in un istante precedente \(\small t - \Delta t\) . Tra le due posizioni successive vi è una distanza angolare \(\small \omega \Delta t\), cioè il vettore tensione \(\small \vec{V}\), partendo dalla posizione \(\small \vec{V}(t - \Delta t)\), giunge in \(\small \vec{V}(t)\) dopo \(\small \Delta t\) secondi, avendo percorso un angolo \(\small \omega \Delta t\).
In questo intervallo di tempo il vettore \(\small \vec{V}(t)\) ha subito una variazione, perchè, pur non essendo cambiato il modulo, sono cambiate la direzione ed il verso. La variazione è a sua volta un vettore :
(37) \( \qquad \qquad \qquad \qquad \qquad \vec{V}(t) - \vec{V}(t - \Delta t) = \Delta \vec{V} \)
o, se si preferisce:
(38) \( \qquad \qquad \qquad \qquad \qquad \vec{V}(t) = \vec{V}(t - \Delta t) + \Delta \vec{V} \)
cioè il vettore in una certa posizione si può ottenere dal vettore in una posizione precedente sommando la variazione \(\small \Delta \vec{V}\).
Anche in questo caso il parametro \(\small \Delta t\) gioca un ruolo critico per la precisione e la consistenza dei risultati.
L'intervallo di tempo \(\small \Delta t\) deve assumere valori molto piccoli, prossimi allo zero. In tal caso il modulo di \(\small \Delta \vec{V}\) risulta praticamente uguale alla lunghezza dell'arco sotteso da \(\small \Delta \vec{V}\) stesso e può essere calcolato come prodotto di raggio x angolo (in radianti). Nel nostro caso il ruolo del raggio è assunto dal modulo del vettore \(\small \vec{V}(t)\) mentre l'angolo è \(\small \omega \Delta t\). Quindi :
(39) \( \qquad \qquad \qquad \qquad \qquad \Delta V = V_M\,\omega\,\Delta t \)
Dalla (30'), che conviene qui scrivere in forma vettoriale:
(40) \( \qquad \qquad \qquad \qquad \qquad \vec{I} = C\, \dfrac{\Delta\,\vec{V}}{\Delta\,t} \)
dove \(\small \vec{V}\) e \(\small \vec{I}\) sono i vettori rotanti che rappresentano le sinusoidi, possiamo ricavare la direzione e il verso della corrente \(\small \vec{I}\), così come il modulo:
(41) \( \qquad \qquad \qquad \qquad \quad I = C\, \dfrac{V_M\,\omega\,\Delta t}{\Delta\,t} = \omega\,C\,V_M \)
Notiamo che mentre \(\small \Delta V\) dipende dall'intervallo temporale \(\small \Delta t\), non è così per \(\small I\), come risulta dalla (41).
ll vettore \(\small \vec{I}\) può essere applicato nell'origine mediante traslazione, in modo da rappresentare più agevolmente la sinusoide \(\small i(t)\).
Osserviamo ora che diminuendo il valore di \(\small \Delta t\), il vettore \(\small \vec{I}\) tende a disporsi perpendicolarmente rispetto a \(\small \vec{V}\). Ciò spiega il fatto che la corrente risulta essere in anticipo di \(\small \dfrac{\pi}{2}\) sulla tensione.
Viene anche messo in evidenza come l'angolo di sfasamento reciproco \(\small \varphi\) approssimi sempre meglio l'angolo retto al diminuire di \(\small \Delta t\).
4.2 - Energia elettrostatica e potenza
 Quando un
condensatore ideale
è collegato ad un generatore di tensione alternata sinusoidale \(\small v(t) = V_M\,sin(\omega t)\), subisce una serie continua di processi di carica e scarica.
La
fase di carica
si ha quando corrente e tensione impressa dal generatore
sono concordi. Nell'esempio della lavagna ciò avviene
durante il primo e, a polarità
invertite, terzo quarto di periodo. In questi intervalli la tensione aumenta, la
corrente diminuisce man mano che si accumula carica sulle armature. La
distribuzione di carica sulle armature forma il campo elettrico
e la relativa differenza di potenziale \(\small v_C(t)\).
Tuttavia quest'ultima, dato che le armature
costituiscono praticamente i terminali del generatore (il circuito è
interrotto dal dielettrico), non può che coincidere con la tensione del
generatore.
Quando un
condensatore ideale
è collegato ad un generatore di tensione alternata sinusoidale \(\small v(t) = V_M\,sin(\omega t)\), subisce una serie continua di processi di carica e scarica.
La
fase di carica
si ha quando corrente e tensione impressa dal generatore
sono concordi. Nell'esempio della lavagna ciò avviene
durante il primo e, a polarità
invertite, terzo quarto di periodo. In questi intervalli la tensione aumenta, la
corrente diminuisce man mano che si accumula carica sulle armature. La
distribuzione di carica sulle armature forma il campo elettrico
e la relativa differenza di potenziale \(\small v_C(t)\).
Tuttavia quest'ultima, dato che le armature
costituiscono praticamente i terminali del generatore (il circuito è
interrotto dal dielettrico), non può che coincidere con la tensione del
generatore. Anche in questo caso lo sfasamento tra tensione e corrente è sintomo dell'attitudine del sistema ad accumulare energia.
La fase di scarica si ha quando tensione impressa e corrente hanno versi discordi. Ciò avviene durante il secondo e quarto quarto di periodo. L'energia precedentemente accumulata nel campo elettrostatico viene restituita al generatore.
L' energia \(\small w\) immagazzinata nel volume di spazio occupato dal campo elettrostatico, posto \(\small v_c(t) = v(t)\) per quanto detto sopra, è:
(42) \( \qquad \qquad \qquad \qquad \quad w(t) = \dfrac{1}{2}\,C\, v^2(t) \)
che si può ottenere, ad esempio, integrando la potenza:
(43) \( \qquad \qquad \qquad p(t) = v(t)\,i(t) = v(t)\,C\,\dfrac{d\,v(t)}{d\,t} = C\,v(t)\,\dfrac{d\,v(t)}{d\,t} \)
(44) \( \qquad \qquad \qquad w(t) = \int p(t)\,dt = C\, \int v(t)\,d\,v(t) = \dfrac{1}{2}\,C\,v^2(t) \)
a meno di una costante che può essere zero se si suppone \(\small v(0) = 0\) , cioè condensatore inizialmente scarico.
Ragionando con le differenze finite notiamo che la potenza, per la (30') è data da:
(45) \( \qquad \qquad \qquad p(t) = v(t)\,i(t) = C\,v(t)\,\dfrac{\Delta\,v(t)}{\Delta\,t}\)
da essa ricaviamo la variazione di energia o la quantità di lavoro eseguita nel tempo \(\small \Delta t\):
(46) \( \qquad \qquad \qquad \Delta\,w(t)= p(t)\,\Delta t = C\,v(t)\,\Delta\,v(t)\)
Sommando i vari \(\small \Delta\,w(t)\) per avere l'energia totale otteniamo:
(47) \( \qquad \qquad \qquad w(t) = \sum \Delta\,w(t) = C\,\sum\,v(t)\,\Delta\,v(t) = \dfrac{1}{2}\,C\,v^2(t)\)
nell'ipotesi che all'inizio v(0) = 0 , cioè il condensatore siainizialmente scarico.
Anche in questo caso la potenza necessaria per trasferire l'energia (47) non può essere estratta dal sistema. Con essa non si può eseguire lavoro su qualche sistema esterno.
Una potenza con tali caratteristiche è detta potenza reattiva.
4.3 - La reattanza capacitiva è un numero immaginario
 Abbiamo lo stesso problema che si
presentava per l'induttore.
Abbiamo lo stesso problema che si
presentava per l'induttore.In una relazione tra la tensione e la corrente di un condensatore la reattanza capacitiva \(\small X_C\) non può essere un semplice numero reale dato che dobbiamo tener conto dello sfasamento della corrente, che qui è in quadratura in anticipo sulla tensione. La tensione sulle armature è dunque in ritardo sulla corrente di \(\small \dfrac {\pi}{2}\).
Ricorrendo ai fasori avremo:
(48) \( \qquad \qquad \qquad \qquad \qquad \dot{V} = -j\,X_C\,\dot{I} \)
il segno meno è giustificato dal fatto che la sinusoide tensione si ottiene, a meno della trasformazione del modulo, con una rotazione di fase di \(\small \dfrac {\pi}{2}\) in ritardo (in senso orario) della sinusoide corrente.
5 - Forza elettromotrice o caduta di tensione?
Ogniqualvolta in un utilizzatore elettrico avviene una trasformazione energetica(4) compare ai suoi capi una differenza di potenziale \(\small v(t)\) che può, in generale, essere funzione del tempo. D'altra parte l'assorbimento o la cessione dell'energia \(\small w(t)\) avvengono necessariamente in un certo tempo, il che comporta l'esistenza di una potenza elettrica:(49) \( \qquad \qquad \qquad p(t) = \dfrac{\Delta\,w(t)}{\Delta\,t} = v(t)\,i(t) \)
In tutte le situazioni che abbiamo analizzato , compresa la fem di autoinduzione, la ddp ai capi dell'utilizzatore ha sempre polarità istantanee coincidenti con quelle della tensione impressa dal generatore.
Dal punto di vista dei versi di percorrenza del circuito, questa ddp appare essere sempre opposta a quella del generatore. Normalmente a questa ddp si dà il nome di caduta di tensione che, come detto, è segno della presenza di una trasformazione energetica.
Nel caso particolare dell'induttore però la ddp che si forma per autoinduzione non è direttamente generata dalla corrente o dalle polarità del generatore. Essa è dovuta ad un fenomeno diverso: la variazione di flusso magnetico all'interno dell'induttore. Per tale motivo è considerata a tutti gli effetti come un forza elettromotrice.
6 - Il bipolo R-L serie
 Un bipolo R-L è costituito
da un resistore e da un induttore ideali collegati in serie.
Un bipolo R-L è costituito
da un resistore e da un induttore ideali collegati in serie.Un carico di questo tipo è detto ohmico-induttivo.
La corrente che scorre nei due dispositivi produce gli effetti che abbiamo esposto prima: una caduta di tensione \(\small v_R(t)\) sul resistore e una fem e(t) sull'nduttore

Figura 4 - vL(t)
è la ddp
impressa sull'induttore
Ai capi dell'induttore il generatore rende disponibile una tensione \(\small v_L(t)\) che deve essere uguale e contraria a \(\small e(t)\): \(\small v_L(t)= -e(t)\).
Potrebbe sembrare contraddittorio rappresentare \(\small v_L(t)\) e \(\small e(t)\) con frecce nello stesso verso,tuttavia dobbiamo pensare che in realtà l'induttore è connesso ai terminali A e B di un generatore equivalente, che comprende il generatore ideale di tensione \(\small v(t)\) in serie con la resistenza \(\small R\). Quest'ultima provoca una caduta di tensione \(\small R\,i(t)\). La differenza di potenziale che si forma tra i terminali A e B è la tensione impressa \(\small v_L(t)\) dal generatore sull'induttore:
(50) \( \qquad \qquad \qquad v_L(t)= v(t) - R\,i(t) \)
ovvero:
(51) \( \qquad \qquad \qquad v_L(t)= v(t) - v_R(t) \)
Dalla (51) è evidente che si avrà:
(52) \( \qquad \qquad \qquad v(t) = v_R(t)+ v_L(t) \)
Ora, quest'ultima è una somma di sinusoidi, che può essere rappresentata da una somma di fasori:
(53) \( \qquad \qquad \qquad \dot{V} = \dot{V}_R + \dot {V}_L \)
d'altra parte da (8) e (26) :
(54) \( \qquad \qquad \qquad \dot{V} = R\,\dot{I} + j\,X_L\,\dot{I} \)
in cui \(\small \dot{V_R} = R\,\dot{I}\) e \(\small \dot{V_L} = j\,X_L\,\dot{I}\) rappresentano le differenze di potenziale presenti sui dispositivi. Esse danno come somma (vettoriale) la \(\small \dot{V}\) del generatore.
I tre fasori tensione, con \(\small \dot{V}_L\) opportunamente trasposto (vettore tratteggiato), danno luogo al cosiddetto triangolo delle tensioni, in cui \(\small \dot{V}_R\) e \(\small \dot{V}_L\) sono i cateti e \(\small \dot{V}\) l'ipotenusa. L'angolo tra \(\small \dot{V}\) e \(\small \dot{V}_R\) coincide con l'angolo \(\small \varphi\) di sfasamento tra tensione e corrente. Tra gli elementi del triangolo sussistono le note relazioni trigonometriche:
(55) \( \qquad \qquad \qquad V_R = V\, cos(\varphi) \qquad \qquad V_L = V\, sin(\varphi)\)
Raccogliendo il fattore comune I nella (54) si ottiene:
(56) \( \qquad \qquad \qquad \qquad \dot{V} = (R + j\,X_L)\,\dot{I} \)
In parentesi abbiamo l'impedenza del bipolo
(57) \( \qquad \qquad \qquad \qquad \dot{Z} = R + j\,X_L \)
in cui \(\small R\) è la parte reale dell'operatore impedenza e \(\small X_L\) la parte immaginaria.
Quindi:
(58) \( \qquad \qquad \qquad \qquad \dot{V} = \dot{Z}\,\dot{I} \)
Dal triangolo delle tensioni ricaviamo il triangolo delle impedenze, di cui \(\small R\) e \( \small X_L\) costituiscono i cateti e \(\small Z\) l'ipotenusa. Anche qui abbiamo le relazioni trigonometriche (omettiamo le parantesi per semplicità):
(59) \( \qquad R = Z\,cos\,\varphi \qquad X_L = Z\,sin\,\varphi \qquad Z= \sqrt{R^2 + X^2_L} \qquad tan\,\varphi =\dfrac{X_L}{R} \)
Si noti che l'angolo φ che compare nel triangolo delle impedenze è positivo perchè rappresenta un anticipo della tensione sulla corrente. Esso è una caratteristica dell'impedenza e non va confuso con gli angoli di fase dei vettori. L'angolo φ è positivo per una impedenza ohmico-induttiva e può variare solo se si modificano i componenti dell'impedenza stessa.
Si chiarisce ora meglio il ruolo di \(\small \dot{Z}\) come operatore complesso sui fasori nel caso ohmico-induttivo. Esso agendo sul vettore \(\small \dot{I}\):
- ne modifica il modulo,
- cambia la natura della grandezza e quindi la dimensione da ampère a volt,
- agisce sull'angolo di fase incrementandolo (rotazione antioraria) di un angolo \(\small \varphi\), dove: (60) \( \qquad \qquad \qquad \qquad \varphi = arctan \left(\dfrac{X_L}{R}\right) \)
Si possono osservare sulla lavagna a sinistra gli effetti delle variazioni di \(\small R\) e \(\small X_L\).
 Attività 4
Attività 4
Invertendo la formula (58) abbiamo:
(61) \( \qquad \qquad \qquad \qquad \dot{I} = \dfrac{1}{\dot{Z}}\,\dot{V} \)
oppure
(62) \( \qquad \qquad \qquad \qquad \dot{I} = \dot{Y}\,\dot{V} \)
che ci permette di definire l'ammettenza come reciproco dell'impedenza:
(63) \( \qquad \qquad \qquad \qquad \dot{Y} = \dfrac{1}{\dot{Z}} \)
L'ammettenza è allora l'operatore inverso dell'impedenza \(\small \dot{Y} = \dot{Z}^{-1}\), che trasforma il fasore tensione nel fasore corrente.
Come si sa, prodotti e divisioni tra numeri complessi si eseguono più agevolmente se si adotta la forma eponenziale:
(64) \( \qquad \qquad \qquad \qquad V\,e^{j\,\alpha} = Z\,e^{j\,\varphi}\,I\,e^{j\,\beta} \)
o la forma polare secondo Steinmetz:
(65) \( \qquad \qquad \qquad \qquad V \angle \alpha = Z \angle \varphi\,I \angle \beta \)
da cui: \(\small \alpha = \varphi + \beta\).
Per l'ammettenza si ha:
(66) \( \qquad \qquad \qquad \qquad \dot{Y} = \dfrac{1}{Z\,e^{j\,\varphi}} = \dfrac{1}{Z}\,e^{-j\,\varphi} \)
oppure:
(67) \( \qquad \qquad \qquad \qquad \dot{Y} = \dfrac{1}{Z}\, \angle -\varphi \)
D'altra parte \(\small \dot{Y}\) può anche essere espressa in forma algebrica:
(68) \( \qquad \qquad \qquad \qquad \dot{Y} = G\,+\,j\,B \)
da cui con semplici calcoli si ricava per la conduttanza \(\small G\) e la suscettanza \(\small B\):
(69) \( \qquad \qquad \qquad \qquad G = \dfrac{R}{R^2+X^2_L} \qquad B = \dfrac{-X_L}{R^2+X^2_L} \)
6.1 - Potenze nel bipolo R-L serie
Il resistore è caratterizzato dalla potenza attiva:(70) \( \qquad \qquad \qquad \qquad P = V_R\,I = V cos\, \varphi\,I = V\,I\,cos\,\varphi \)
l'induttore dalla potenza reattiva:
(71) \( \qquad \qquad \qquad \qquad Q = V_L\,I = V sin\, \varphi\,I = V\,I\,sin\,\varphi \)
in cui abbiamo usato le (55).
In alternativa, ricordando che in modulo \(\small V_R = R\,I\) e \(\small V_L = X_L\,I\), avremo anche:
(72) \( \qquad \qquad \qquad \qquad P = V_R\,I = R\,I^2 \)
(73) \( \qquad \qquad \qquad \qquad Q = V_L\,I = X_L\,I^2 \)
7 - Il bipolo R-C serie
 Un bipolo R-C è costituito
da un resistore e da un condensatore ideali
collegati in serie. Un carico di questo tipo è detto ohmico-capacitivo.
Un bipolo R-C è costituito
da un resistore e da un condensatore ideali
collegati in serie. Un carico di questo tipo è detto ohmico-capacitivo.La somma delle due ddp deve eguagliare la \(\small v(t)\) del generatore:
(74) \( \qquad \qquad \qquad \qquad v(t) = v_R(t) + v_C(t)\)
che si traduce nella relazione tra fasori:
(75) \( \qquad \qquad \qquad \qquad \dot{V} = \dot{V}_R + \dot{V}_C\)
ricorriamo alle (48) e (8) per scrivere:
(76) \( \qquad \qquad \qquad \qquad \dot{V} = R\,\dot{I} - j\,X_C\,\dot{I}\)
in cui \(\small \dot{V}_R = R\,\dot{I}\) e \(\small \dot{V}_C = - j\,X_C\,\dot{I}\) rappresentano le differenze di potenziale presenti sui dispositivi. Esse danno come somma (vettoriale) la \(\small \dot{V}\) del generatore.
I tre fasori tensione, con \(\small \dot{V}_C\) opportunamente trasposto (vettore tratteggiato), danno luogo al cosiddetto triangolo delle tensioni, in cui \(\small \dot{V}_R\) e \(\small \dot{V}_C\) sono i cateti e \(\small \dot{V}\) l'ipotenusa. L'angolo tra \(\small \dot{V}\) e \(\small \dot{V}_R\) coincide con l'angolo \(\small \varphi\) di sfasamento tra tensione e corrente. Tra gli elementi del triangolo sussistono le note relazioni trigonometriche:
(77) \( \qquad \qquad \qquad V_R = V\, cos(\varphi) \qquad \qquad V_C = V\, sin(\varphi)\)
Raccogliendo \(\small \dot{I}\) nella(76):
(78) \( \qquad \qquad \qquad \qquad \dot{V} = (R - j\,X_C)\,\dot{I}\)
mentre l'impedenza è:
(79) \( \qquad \qquad \qquad \qquad \dot{Z} = R - j\,X_C\)
È bene notare che la parte immaginaria di \(\small \dot{Z}\) negativa comporta che l'angolo \(\small \varphi\) sia a sua volta negativo:
(80) \( \qquad \qquad \qquad \qquad \varphi = arctan\left( \dfrac{-X_C}{R} \right)\)
Nel caso ohmico-capacitivo l'operatore \(\small \dot{Z}\), agendo sul vettore \(\small \dot{I}\)>:
- ne modifica il modulo,
- cambia la natura della grandezza e quindi la dimensione da ampère a volt,
- agisce sull'angolo di fase decrementandolo (rotazione oraria) di un angolo \(\small \varphi = arctan\left( \dfrac{-X_C}{R} \right)\)
 Attività 5
Attività 5
Per l'ammettenza si ha:
(81) \( \qquad \qquad \qquad \qquad \dot{Y} = \dfrac{1}{Z\,e^{-j\,\varphi}} = \dfrac{1}{Z}\,e^{j\,\varphi} \)
oppure:
(82) \( \qquad \qquad \qquad \qquad \dot{Y} = \dfrac{1}{Z}\, \angle \varphi \)
D'altra parte \(\small \dot{Y}\) può anche essere espressa in forma algebrica:
(83) \( \qquad \qquad \qquad \qquad \dot{Y} = G\,+\,j\,B \)
da cui con semplici calcoli si ricava per la conduttanza \(\small G\) e la suscettanza \(\small B\):
(84) \( \qquad \qquad \qquad \qquad G = \dfrac{R}{R^2+X^2_C} \qquad B = \dfrac{X_C}{R^2+X^2_C} \)
Notiamo anche qui le differenze di segno della suscettanza rispetto al caso ohmico-induttivo.
7.1 - Potenze nel bipolo R-C serie
Il resistore è caratterizzato dalla potenza attiva:(85) \( \qquad \qquad \qquad \qquad P = V_R\,I = V cos\, \varphi\,I = V\,I\,cos\,\varphi \)
il condensatore dalla potenza reattiva:
(86) \( \qquad \qquad \qquad \qquad Q = - V_C\,I = - V sin\, \varphi\,I = - V\,I\,sin\,\varphi \)
in cui abbiamo usato le (77).
In alternativa, ricordando che in modulo \(\small V_R = R\,I\) e \(\small V_C = X_C\,I\), avremo anche:
(87) \( \qquad \qquad \qquad \qquad P = V_R\,I = R\,I^2 \)
(88) \( \qquad \qquad \qquad \qquad Q = -V_C\,I = - X_C\,I^2 \)
Come si vede la potenza reattiva capacitiva, date le relazioni tra le grandezze in gioco, è negativa.
Quest'ultima affermazione può essere meglio compresa se si prende come riferimento la corrente, sia nel caso R-C che nel caso R-L (si vari l'angolo α fino ad avere il vettore corrente giacente sull'asse reale e quindi con fase nulla): \(\small V_L\) e \(\small V_C\) sono opposti, \(\small V_L\) è positivo, \(\small V_C\) è negativo. La potenza reattiva induttiva è positiva, la potenza reattiva capacitiva è negativa.
8 - Il bipolo R-L-C serie
 Nel bipolo R-L-C abbiamo
tutti e tre i componenti fondamentali collegati in serie.
Nel bipolo R-L-C abbiamo
tutti e tre i componenti fondamentali collegati in serie.Grazie alle conoscenze finora acquisite siamo in grado di scrivere direttamente l'impedenza:
(89) \( \qquad \qquad \qquad \qquad \dot{Z} = R + j\,X_L - j\,X_C = R + j\,(X_L - X_C)\)
A seconda dei valori che assumono le reattanze, la corrente può essere
- in anticipo
- in fase
- in ritardo
Quindi il carattere del bipolo può essere globalmente di tipo:
- capacitivo
- resistivo
- induttivo
Di particolare interesse, per le implicazioni relative allo sfruttamento efficiente della potenza elettrica(5), è il caso in cui \(\small X_L = X_C\), che, come si può vedere dalla (89), comporta l'annullamento della parte immaginaria dell'impedenza. Il carico allora appare essere di tipo resistivo, pur essendo presenti un induttore e un condensatore.
 Attività 6
Attività 6
Le differenze di potenziale presenti sui dispositivi danno come somma (vettoriale) la V del generatore.
8.1 - Scambi energetici nel bipolo R-L-C serie
Nelle precedenti analisi abbiamo evidenziato il comportamento energetico dei vari dispositivi. Riassumiamo:- Il resistore trasforma energia in calore senza accumularla. La potenza è di tipo attivo:fluisce solamente dal generatore all'utilizzatore. La potenza fuoriesce dal sistema (come calore in questo caso).
- L'induttore accumula energia sotto forma di campo magnetico in determinati intervalli di tempo. L'energia viene restituita al generatore durante altri intervalli. Non vi è alcuna dissipazione. La potenza fluisce nei due sensi ed è di tipo reattivo. Non può uscire dal sistema. Non può eseguire lavoro all'esterno del sistema
- Il condensatore accumula energia sotto forma di campo elettrico in determinati intervalli di tempo. L'energia viene restituita al generatore durante altri intervalli. Non vi è alcuna dissipazione. La potenza fluisce nei due sensi ed è di tipo reattivo. Non può uscire dal sistema. Non può eseguire lavoro all'esterno del sistema
Ciò può essere compreso osservando la disposizione dei vettori tensione e corrente sui dispositivi, la cui relazione con l'energia e la potenza abbiamo discusso precedentemente.
In altre parole induttore e condensatore hanno comportamento complementare. Quindi tutta o parte dell'energia e della potenza reattiva possono essere scambiate tra loro, coinvolgendo solo in parte o per nulla (quando XL = XC) il generatore.
 Attività 7
Attività 7
9 - Risonanza di tensione.
 È molto interessante analizzare il comportamento delle reattanze induttiva e
capacitiva al variare della frequenza.
È molto interessante analizzare il comportamento delle reattanze induttiva e
capacitiva al variare della frequenza.
Dalla figura 5, considerate anche le ormai note espressioni delle reattanza induttiva e capacitiva, che qui riportiamo:
\( \qquad \qquad \qquad \qquad \qquad X_L = 2\,\pi\,L\,f \)
\( \qquad \qquad \qquad \qquad \qquad X_C = \dfrac{1}{2\,\pi\,C\,f} \)
possiamo osservare che la reattanza induttiva ha andamento lineare, crescente con la frequenza, mentre la reattanza capacitiva ha andamento iperbolico, essendo inversamente proporzionale alla frequenza.
Ancora, possiamo notare che per \(\small f = 0\) Hz, corrispondente ad una corrente continua, l'induttore ideale è assimilabile a un corto circuito: \( \small X_L = 0\), mentre il condensatore ideale rappresenta una interruzione, cioè un circuito aperto: \(\small X_C = \infty\).
Un circuito con un induttore in serie tende a tagliare le alte frequenze in misura tanto maggiore quanto più elevata è l'induttanza (filtro passa-basso). Un condensatore in serie taglia invece le basse frequenze, tanto più, quanto minore è la capacità C (filtro passa-alto).
Figura 5 - Andamento delle reattanze induttiva e capacitiva in funzione della frequenza
Esiste un valore della frequenza, detto frequenza di risonanza \(\small f_R\) per cui le due curve si intersecano. Per questa frequenza le due reattanze hanno lo stesso valore: \(\small X_L = X_C\), l'impedenza \(\small Z = R + j\,( X_L - X_C)\) assume il valore minimo, pari a \(\small R\). Conseguentemente la corrente presenta un massimo.
Diciamo allora che il sistema è in risonanza. Nel caso presente si parla di risonanza serie o risonanza di tensione.
In risonanza la corrente è limitata dalla sola resistenza, mentre tensione impressa e corrente sono rigorosamente in fase.
 Attività 8: la risonanza
Attività 8: la risonanza
Dal punto di vista energetico possiamo dire che la condizione di risonanza è caratterizzata dall'equilibrio nello scambio di potenza tra i componenti reattivi. Le due potenze sono uguali e di segno opposto, segno che mentre un componente assorbe energia (potenza) reattiva l'altro la cede nella quantità esattamente necessaria. Il sistema diventa indipendente dal generatore relativamente alla potenza reattiva.
Esiste ovviamente una formula che permette di determinare il valore \(\small f_R\), note \(\small L\) e \(\small C\).
Se \(\small X_L = X_C\), abbiamo \(\small 2\,\pi\,L\,f= \dfrac{1}{2\,\pi\,C\,f}\) e quindi \(\small (2\,\pi)^2\,L\,C\,f^2 = 1\), da cui otteniamo per la frequenza di risonanza:
(90) \( \qquad \qquad \qquad \qquad f_R = \dfrac{1}{2\,\pi\,\sqrt{L\,C}}\)
La condizione di risonanza di tensione è potenzialmente pericolosa, dato che anche con tensioni di alimentazione di modesta entità, si possono presentare correnti elevate che, sui componenti reattivi (induttore e condensatore), generano differenze di potenziale anche molto elevate. Questo succede perchè l'eguaglianza delle reattanze, con conseguente annullameno della parte immaginaria dell'impedenza, fa sì che sia solo la resistenza a limitare la corrente. Se \(\small R\) è molto piccola la corrente è proporzionalmente intensa. Al limite per \(\small R = 0\) si avrebbe una condizione di corto circuito con corrente e tensioni tendenti a valori infinitamente grandi.
 Attività 9
Attività 9
Di fatto l'impedenza presenta il valore minimo in corrispondenza della frequenza di risonanza, a cui corrisponde un massimo dell'intensità di corrente.
Non solo l'impedenza dipende dalla frequenza, ma anche il suo angolo caratteristico \(\small \varphi\).
Figura 6 - Andamento della impedenza e dell'angolo di fase in funzione della frequenza
L'angolo \(\small \varphi\) dell'impedenza subisce una rotazione al variare della frequenza, come evidenziato dalla figura 6. Il passaggio per lo zero avviene esattamente alla frequenza di risonanza. A destra della frequenza di risonanza, l'angolo \(\small \varphi\) è positivo e il carattere del bipolo è ohmico-induttivo (o semplicemente induttivo se R=0), a sinistra della frequenza di risonanza \(\small \varphi\); è negativo, il bipolo ha carattere ohmico-capacitivo. Alla frequenza di risonanza \(\small \varphi = 0\). Il bipolo ha un comportamento di tipo ohmico. Possiamo anche studiare il comportamento in frequenza nel caso R-L ove si nota chiaramente l'effetto di attenuazione alle alte frequenze della corrente, e il caso R-C, per cui l'attenuazione si ha alle basse frequenze.
 Attività 10
Attività 10
Modulo successivo: Modulo precedente:
Rev. gennaio 2021
Testi dell'autore e approfondimenti
(1) Quasi sempre si confonde il dispositivo, il resistore, con la sua caratteristica elettrica: la resistenza. Ciò accade anche con induttore (dispositivo) e induttanza (caratteristica). Mentre con condensatore si indica correttamente il dispositivo e con capacità la caratteristica elettrica

(2) Un solenoide di \(\small N \) spire, sezione \(\small S\) e lunghezza \(\small l\) produce un flusso magnetico \(\small \Phi = \mu\,\dfrac{S}{l}\,N\,I\ = \dfrac{N\,I}{\mathcal{R}} \), dove \(\small \mathcal{R}\) è la riluttanza magnetica, quando è percorso da una corrente elettrica di intensità \(\small I\). Il flusso concatenato è \(\small N\) volte il flusso \(\small \Phi\), dato che si concatena con le stesse \(\small N\) spire: \(\small \Phi_C = \dfrac{N^2}{\mathcal{R}}\,I = L\,I \)

(3) Eccezionalmente e in deroga alla convenzioni tipografiche usiamo qui anche \(\small \vec{I}(t)\) e \(\small \vec{I}(t - \Delta t)\) per esprimere la dipendenza dal tempo della posizione del vettore rotante.

(4) Una trasformazione energetica in un circuito elettrico comporta un moto di cariche, e quindi una corrente \(\small i(t)\), tra due punti A e B di un circuito elettrico, tra i quali vi sia differenza di potenziale \(\small V_{AB}\). A presenta una polarità istantanea positiva se, rispetto ad un riferimento comune per il potenziale, \(\small V_A(t) > V_B(t)\). Altrimenti si avrà su A una polarità istantanea nulla se \(\small V_A(t)= V_B(t)\), o negativa se \(\small V_A(t) < V_B(t)\).

(5) La tecnica di portare la corrente in fase con la tensione è detta rifasamento. Con ciò si migliora lo sfruttamento dell'energia elettrica da parte degli impianti. Nelle applicazioni pratiche si collega un condensatore non in serie, ma in parallelo ad un carico ohmico-induttivo, perchè è necessario non variare la tensione sul carico, per non modificarne le caratteristiche di funzionamento.

 Nell'esempio
abbiamo inizialmente fissato \(\small R = 4 \quad \Omega \), valore efficace della tensione \(\small V = 24 \quad V\), cui corrisponde
un'ampiezza \(\small V_M = 33,9 \quad V\).
Il valore della resistenza può essere variato attraverso il cursore
(slider) \(\small \,"R"\) che
compare in basso a sinistra. Il motivo per cui nella scrittura
dell'
Nell'esempio
abbiamo inizialmente fissato \(\small R = 4 \quad \Omega \), valore efficace della tensione \(\small V = 24 \quad V\), cui corrisponde
un'ampiezza \(\small V_M = 33,9 \quad V\).
Il valore della resistenza può essere variato attraverso il cursore
(slider) \(\small \,"R"\) che
compare in basso a sinistra. Il motivo per cui nella scrittura
dell' chiudi questo riquadro
chiudi questo riquadro