I NUMERI COMPLESSI seconda parte

La formula e l'identità di Eulero. Potenze e logaritmi complessi
Discipline: Matematica
Sintesi:
La formula
di Eulero-Cotes, un 'gioiello matematico' secondo il nobel Richard
Feynman, ha un ruolo fondamentale in molte appplicazioni della fisica:
dallo studio delle onde, alla meccanica quantistica, alla risoluzione
delle equazioni differenziali. Vedremo anche come
definire l'elevamento a potenza con esponente complesso, il logaritmo e
analizzeremo le interessanti proprietà di
queste entità.
2.1 - Il numero complesso \( cos \; \alpha + i\; sin\; \alpha \)
La particolare importanza che questo numero ricopre nella rappresentazione dei numeri complessi, ci induce a rivedere e ad approfondire alcune sue importanti proprietà.Con lo scopo di alleggerire la notazione useremo d'ora in poi \( cos \; \alpha + i\; sin\; \alpha \) in luogo della più corretta espressione \( cos \; (\alpha) + i\; sin\; (\alpha) \) e così per tutte le funzioni trigonometriche, ove non siano possibili ambiguità.
2.1.1 - Altre proprietà di \( cos \; \alpha + i\; sin\; \alpha \)
 Torniamo dunque al numero complesso \( cos \; \alpha + i\; sin\; \alpha \).
Torniamo dunque al numero complesso \( cos \; \alpha + i\; sin\; \alpha \).
Come abbiamo visto nella prima parte, esso consente di rappresentare qualsiasi numero complesso \( \dot{z}= r_z\; (cos \; \alpha + i\; sin\; \alpha) \), se moltiplicato per il suo modulo \(r_z = |\dot{z}| \).
Ma esistono altri aspetti interessanti di questo oggetto che vale la pena di indagare.
Per comodità di rappresentazione poniamo \( \dot{u_{\alpha}} = cos \; \alpha + i\; sin\; \alpha \).
Usiamo a questo scopo la lettera \(u \) che ci ricorda l'unità, essendo infatti unitario il modulo: \( |\dot{u_{\alpha}}|^2 = cos^2 \; \alpha + sin^2 \; \alpha = 1 \), e l'indice \(\alpha \) per evidenziare l'argomento .
L'argomento di \(u_{\alpha} \), indicato con \(Arg(u_{\alpha}) \) è l'angolo \(\alpha \), misurato in radianti. Esso può assumere tutti i valori tra \(0 \) e \(2 k \pi \), con \(k = 1, 2, ... \), numero intero. Spesso, per eliminare l'ambiguità dovuta alla periodicità delle funzioni seno e coseno, lo si limita all'intervallo \(-\pi\; \leq \;\alpha\; \leq\; \pi \). In questo caso si indica con \(arg(u_{\alpha})\), e viene detto determinazione o valore principale dell'argomento.
Il complesso coniugato di \(u_{\alpha} \) è evidentemente: \( \dot{u^*_{\alpha}} = cos \; \alpha - i\; sin\; \alpha\), ma la cosa interessante è che esso coincide con il reciproco di \(u_{\alpha} \):
\( \frac{1}{\dot{u_{\alpha}}} =\frac{1}{ cos \;\alpha + i\; sin\;\alpha}= \frac{cos\;\alpha - i\; sin\; \alpha}{(cos\;\alpha + i\; sin\;\alpha)(cos \;\alpha - i\; sin\;\alpha)} = \frac{cos\;\alpha - i\; sin\; \alpha}{(cos^2 \;\alpha + sin^2\; \alpha)} = cos \; \alpha - i\; sin\; \alpha\)
Quindi: \[\dot{u}^*_{\alpha} = \frac{1}{\dot{u}_{\alpha}} \] La formula di De Moivre (par. 1.4.3 - 1° capitolo): \[ (cos \; \alpha + i\; sin\; \alpha)^n = cos \;n \alpha + i\; sin\; n \alpha\] consente di calcolare facilmente la potenza ennesima di \(u_{\alpha} \).
Qui si evidenzia un comportamento singolare di \(Arg(u_{\alpha}) \), reso più evidente dalla rappresentazione in forma polare \(\dot{u}_{\alpha} = 1\; \angle\; \alpha \) :
\[(\dot{u}_{\alpha})^n = (1\; \angle\; \alpha)^n = 1^n \;\angle\;n\alpha = 1 \;\angle\; \alpha+\alpha+\alpha+... = 1 \;\angle\; \sum_{1}^n \alpha \] ovvero: \[ 1 \;\angle \;\alpha \cdot 1 \;\angle \;\alpha \cdot 1 \;\angle \;\alpha\;\cdot ... = 1\; \angle\; \alpha + \alpha + \alpha+ ... \quad (n\; volte)\]
In questo contesto, \(Arg(u_{\alpha}) \) sembra comportarsi in modo simile ad un logaritmo, nel senso che, da un prodotto di n grandezze dipendenti da \(\alpha \) si ottiene una grandezzavrisultante, che dipende dalla somma di n addendi \(\alpha \). Questo non può non far pensare, in qualche modo, ai logaritmi, che godono proprio della proprietà di convertire la somma in prodotto (1):
Il legame tra \(\alpha = Arg(u_{\alpha}) \) e i logaritmi di numeri complessi effettivamente esiste, ma non è così semplice ed evidente come nel caso dei numeri reali. Lo approfondiremo nel seguito.
2.1.2 - Il prodotto \(\dot{u}_{\alpha} \cdot \dot{u}_{\beta}\)
La formula di De Moivre risolve il caso particolare del calcolo di potenze di \(\dot{u}_{\alpha} \) e cioè del prodotto di \(\dot{u}_{\alpha} \) per se stesso n volte. Nel 1° capitolo abbiamo dimostrato che, in generale, il prodotto di due numeri complessi si ottiene moltiplicando tra loro i moduli e sommando gli argomenti: \[\dot{u}_{\alpha} \cdot \dot{u}_{\beta} = 1 \angle \;\alpha \cdot 1 \angle \;\beta = 1 \angle \; \alpha+\beta\] Pensiamo ora ad \(\alpha \) e \(\beta \) come a due variabili reali e, per rafforzare questa idea, diamo loro i nomi x e y. Scriveremo allora: \[ \dot{u}(x) = cos \; x + i\; sin\; x \quad \dot{u}(y) = cos \; y + i\; sin\; y \] mettendo in evidenza la dipendenza dagli argomenti x e y, che ovviamente rappresentano angoli. Per quanto precedentemente detto e dimostrato troviamo che: \[\dot{u}(x) \cdot \dot{u}(y) = \dot{u}(x+y)\] Tra le fuzioni reali di variabile reale che conosciamo, esiste una funzione dal comportamento simile: la funzione esponenziale \(a^x \) \[a^x \cdot a^y = a^{x+y}\] la domanda che a questo punto sorge spontanea è: "esiste forse una qualche correlazione tra \( cos \; x + i\; sin\; x\) e la funzione esponenziale?"Prima di dare una risposta occupiamoci di un'altra importante caratteristica di \(\dot{u}_{\alpha} \).
2.1.3 - La derivata di \( \dot{u}(x) = cos \; x + i\; sin\; x\) rispetto al suo argomento
Per una migliore comprensibilità, aiutiamoci anche qui con la più familiare notazione funzionale \( \dot{u}(x)\). Calcoliamo quindi la derivata \( \dot{u}'(x)\) rispetto ad x applicando le normali regole di derivazione:\[ \dot{u}'(x) = \frac{d}{dx}(cos\; x + i\; sin\; x) = \frac{d\; cos\; x}{dx} + i\; \frac{d\; sin\;x}{dx} = - sin\; x + i \; cos\; x\] essendo \( i^2 = -1\), abbiamo che \( -sin x = i^2 sin x\) per cui, raccogliendo \(i^2\):
\[ \frac{d}{dx}(cos\; x + i\; sin\; x) = i^2\: sin\; x + i \; cos\; x = i\;(cos\;x + i\;sin\;x) \] e infine: \[ \dot{u}'(x) = i\;\dot{u}(x)\] Dunque eseguire la derivata di \( \dot{u}\) rispetto al suo argomento equivale a moltiplicare \( \dot{u}\) per l'unità immaginaria, ottenendo \( \dot{u}'= i \cdot u\)
Dal punto di vista vettoriale sappiamo che ciò significa ruotare \( \dot{u}\) di 90° in senso antiorario. D'altra parte se deriviamo ulteriormente, avremo: \[ \dot{u}''(x) = \frac{d^2\;\dot{u}(x)}{dx^2} \ = \frac{d \dot{u}'(x)}{dx} = i\;\frac{d \dot{u}(x)}{dx} = i^2\;\dot{u}(x) \] e, in generale: \[ \dot{u}^{(n)}(x) = \frac{d^n}{dx^n} \dot{u}(x) = i^n\;\dot{u}(x) \] la derivata di ordine n di \( \dot{u}(x)\) è data da \( \dot{u}(x)\) moltiplicato per l'ennesima potenza dell'unità immaginaria.
Questo comportamento è sorprendentemente simile a quello della funzione esponenziale \( e^{cx}\): \[ \frac{d^n\;e^{c x}}{dx^n} = c^n\;e^{c x} \quad c,\;x:\; reali,\; n= 1, 2, 3,..\] Se fosse possibile porre \( c = i\), il che comporta di poter definire un esponenziale con esponente immaginario \( e^{i x}\), la corrispondenza sarebbe completa.
2.2 - La formula di Eulero
2.2.1 - Derivazione della formula di Eulero-Cotes
Osservando le proprietà di \( \dot{u}_\alpha = cos \; \alpha + i\; sin\; \alpha\) abbiamo avuto diversi segnali che ci inducono a immaginare l'esistenza di una profonda relazione tra di esso e la funzione esponenziale. Riassumiamo questi indizi:- l'argomento α tende a comportarsi come un logaritmo e quindi come un esponente;
- il prodotto segue le regole tipiche degli esponenziali;
- la derivazione dà un risultato simile a quello ottenuto derivando l'esponenziale \( e^{c x}\).
Nel paragrafo 1.5.5 del 1° capitolo abbiamo trovato l'espressione delle radici n-sime di un numero complesso. Nel caso particolare di \( \dot{u}_\alpha\):
\[\sqrt[n]{\dot u}_\alpha = \dot{u}_\alpha^{\frac{1}{n}} = cos \frac{ \alpha +2 k \pi}{n} + i\;sin \frac{ \alpha +2 k \pi}{n} \hspace{1cm} k = 0, 1, 2, ..., n-1 \] limitandoci a k = 0 determiniamo \(\dot{u}_\alpha^{\frac{1}{n}} \) \[\dot{u}_\alpha^{\frac{1}{n}} = cos \frac{ \alpha}{n} + i\;sin \frac{ \alpha}{n} \] Elevando alla n-sima potenza riotteniamo \( \dot{u}_\alpha\), essendo l'elevamento a potenza n-sima operazione inversa rispetto all'estrazione di radice n-sima: \[\left(\dot{u}_\alpha^{\frac{1}{n}} \right)^n = \left( cos \frac{ \alpha}{n} + i\;sin \frac{ \alpha}{n}\right)^n = cos \frac{ n\;\alpha}{n} + i\;sin \frac{ n\;\alpha}{n} = \dot{u}_\alpha \] Quindi, per ogni n intero è sempre verificato che:
\[ \left( cos \frac{ \alpha}{n} + i\;sin \frac{ \alpha}{n}\right)^n = cos \;\alpha+ i\;sin \alpha \] Immaginiamo ora di aumentare il valore di n in modo che assuma valori sempre più grandi.
L'operazione matematica è il passaggio al limite per n tendente ad infinito:
\[ \lim_{n \to \infty}{ \left( cos \frac{ \alpha}{n} + i\;sin \frac{ \alpha}{n}\right)^n} = cos \;\alpha+ i\;sin \alpha \] In tal caso \[ \lim_{n \to \infty}{\frac{ \alpha}{n}}= 0 \quad \Rightarrow \quad \left( \lim_{n \to \infty} {cos \frac{ \alpha}{n}}=1\; \wedge\; \lim_{n \to \infty} {sin \frac{ \alpha}{n}} = \frac{ \alpha}{n} \right) \] Allora diviene possibile scrivere
\[ \lim_{n \to \infty}{ \left( cos \frac{ \alpha}{n} + i\;sin \frac{ \alpha}{n}\right)^n} = \lim_{n \to \infty}{\left(1 +\frac{i\; \alpha}{n}\right)^n} \] Com'è noto la definizione di esponenziale di esponente reale è:
\[e^x = \lim_{n \to \infty}{\left(1 +\frac{x}{n}\right)^n} \] e se poniamo \( x= i\;\alpha\) abbiamo la definizione di esponenziale di argomento immaginario:
\[ e^{i \alpha} = \lim_{n \to \infty}{\left(1 +\frac{i\; \alpha}{n}\right)^n} \] Così possiamo finalmente scrivere la formula di Eulero - Cotes(2):
| \[ e^{i \alpha} = cos \;\alpha + i\;sin\; \alpha \] |
Come abbiamo potuto verificare nei precedenti paragrafi, tutte le proprietà tipiche della funzione esponenziale sono verificate.
Questa formula costituisce un importante anello di congiunzione tra algebra e geometria. Le sue implicazioni sono notevolissime in tutti i campi della scienza.
Le sue proprietà sono particolarmente utili nello studio delle oscillazioni e delle onde.
 La lavagna a sinistra consente di evidenziare il comportamento del numero complesso
\(\left(1 +\frac{i\; \alpha}{n}\right)^n \)
al variare del parametro n.
La lavagna a sinistra consente di evidenziare il comportamento del numero complesso
\(\left(1 +\frac{i\; \alpha}{n}\right)^n \)
al variare del parametro n.Per ogni valore di n sono visualizzabili anche i punti rappresentativi delle varie potenze del numero stesso:
\[ \dot{p}_n^k=\left(1 +\frac{i\; \alpha}{n}\right)^k \quad k=1, 2, ..., n \] Ad esempio fissato n = 3 avremo sul piano di Gauss rappresentati: \( \dot{p}_3^1=\left(1 +\frac{i\; \alpha}{3}\right)^1 \quad \dot{p}_3^2=\left(1 +\frac{i\; \alpha}{3}\right)^2 \quad \dot{p}_3^3=\left(1 +\frac{i\; \alpha}{3}\right)^3 \) È interessante notare come, al crescere di n, tutti i punti tendano a sistemarsi sulla circonferenza unitaria e \(\dot{p}^n_n\) tenda ad \( \dot{u}_\alpha\). Ciò rende anche visivamente l'idea che effettivamente, al crescere di n, sempre meglio \(\left(1 +\frac{i\; \alpha}{n}\right)^n \) approssima l'operatore di rotazione di \(\alpha \) radianti (vedere anche il successivo paragrafo 2.2.2).
La simulazione è impostata inizialmente con \( \alpha = \pi\) approssimando così, al crescere di n, l'identità di Eulero \(e^{i \pi} = -1\) (vedere paragrafo 2.2.3). È ovviamente possibile variare \( \alpha\), muovendo il punto sulla circonferenza.
[ Consiglio: seleziona con il mouse il punto n sullo slider e poi muovi con i tasti ← → della tastiera ]
Considerando il complesso coniugato di \( \dot{u}_\alpha\), \( \dot{u}^*_\alpha = cos \; \alpha - i\; sin\; \alpha\) si giunge alla:
\[ e^{i \alpha} = \lim_{n \to \infty}{\left(1 -\frac{i\; \alpha}{n}\right)^n} = cos \; \alpha - i\;sin\;\alpha \]
e quindi:
| \[ e^{-i \alpha} = cos \;\alpha - i\;sin \alpha \] |
Dalle formule precedenti si ricava immediatamente che:
\[ \frac{e^{i \alpha} + e^{-i \alpha}}{2} = cos \;\alpha \quad \quad \frac{e^{i \alpha} - e^{-i \alpha}}{2 i} = sin \alpha \]
Concludiamo riassumendo due proprietà fondamentali dell'esponenziale di esponente immaginario:
a) prodotto di esponenziali: \[ e^{i \alpha} \cdot e^{i \beta} = e^{i \alpha + i \beta}= e^{i (\alpha+\beta)} \] b) derivata di ordine n dell'esponenziale \[ \frac{d^{(n)} e^{i \alpha}}{d \alpha^n} = i^n\; e^{i \alpha}\]
2.2.2 - L'operatore di rotazione \( e^{i \alpha} \)
Se \(\alpha = \frac{\pi}{2}\) abbiamo \( e^{i \frac{\pi}{2}} = cos \;\frac{\pi}{2} + i\;sin \frac{\pi}{2}= 0 + i \;1 = i\) e quindi:| \[ e^{i \frac{\pi}{2}} = i\] |
Quest'ultima formula ci conferma che \( e^{i \frac{\pi}{2}}\) può essere interpretato come un operatore di rotazione di \(\frac{\pi}{2}\) radianti.
Moltiplicare qualsiasi numero complesso per \( e^{i \frac{\pi}{2}}\) equivale a moltiplicarlo per i e quindi a incrementare l'argomento di\(\frac{\pi}{2}\) radianti. Ciò significa ruotare di 90° antiorari il vettore rappresentativo.
Allo stesso modo, e più in generale, \( e^{i \alpha} \) produrrà una rotazione di \(\alpha \) radianti. Se, ad esempio \(\dot{z} = z\; \angle \; \beta\) avremo: \[ e^{i \alpha} \cdot \dot{z}= z\; \angle \; \beta + \alpha\]
2.2.3 - L'dentità di Eulero
Se \(\alpha = \frac{\pi}{2}\) allora \( e^{i \pi} = cos \;\pi + i\;sin \pi = -1\) e la formula di Eulero assume l'aspetto della celebre identità di Eulero,| \[ e^{i \pi} + 1 = 0\] |
Essa rappresenta una specie di totem della conoscenza matematica poichè contiene i cinque numeri fondamentali:
| 0 | lo zero, che consente la moderna notazione posizionale; | 1 | il primo numero della successione dei numeri naturali; | π | il rapporto tra circonferenza e diametro; | e | il numero di nepero, base dei logaritmi naturali; | i | l'unità immaginaria; | +,x,= | le operazioni fondamentali prodotto, somma e il segno di uguaglianza; |
inoltre essa pone in relazione la Geometria e l'Algebra, attraverso \(\pi\)(3) numero fondamentale per la geometria euclidea, e \( i\) unità immaginaria.
2.2.4 - Forma esponenziale dei numeri complessi
Le considerazioni precedenti ci consentono di individuare una nuova forma per i numeri complessi: la forma esponenziale.Se è vero che ogni numero complesso può essere espresso nella forma \( \dot{z}= r_z\; (cos \; \alpha + i\; sin\; \alpha) \), la formula di Eulero ci dà modo di esprimere ogni numero complesso nella cosiddetta forma esponenziale:
| \[\dot{z} = r_z\; e^{i \alpha}\] |
dove rz è il modulo del numero complesso e α il suo argomento.
Il complesso coniugato è:
| \[\dot{z}^* = r_z\; e^{-i \alpha}\] |
Notiamo che \[\dot{z} \cdot \dot{z}^* = r_z^2\; e^{i (\alpha - \alpha)} = r_z^2\; e^{i 0} = r_z^2\] dove per definizione: \( e^{i 0} = 1\)
2.2.5 - Operazioni con numeri complessi in forma esponenziale
Dati due numeri complessi in forma esponenziale \(\dot{z} = r_z\; e^{i \alpha}\) e \(\dot{w} = r_w\; e^{i \beta}\) l' operazione di moltiplicazione diviene:| \[\dot{z} \cdot \dot{w} = r_z\; e^{i \alpha} \cdot r_w\; e^{i \beta} = r_z r_w\; e^{i (\alpha + \beta)} \] |
Il reciproco di un numero comnplesso, ad esempio \(\dot{w}\) è dato da:
| \[ \dot{w}^{-1} = \frac{1}{ r_w\; e^{i \beta}} = \frac{1}{r_w}\; e^ {-i\beta} \] |
di conseguenza la divisione tra numeri complessi in forma esponenziale:
| \[\frac{\dot{z}}{\dot{w}} = \frac{r_z}{ r_w} e^{i (\alpha - \beta)} \] |
L' elevamento alla potenza n-sima con n intero è ovvia conseguenza della moltiplicazione:
| \[\dot{z}^n = r_z^n\; e^{i n \alpha} \] |
Da quest'ultima si può facilmente ricavare la formula di De Moivre.
Per quanto riguarda l'estrazione di radice n-sima :
| \[\sqrt[n]{\dot{z}} = \sqrt[n]{r_z}\; e^{i \frac{\alpha + 2 k \pi}{n}} \] |
con l'intero k = 0, 1, 2, ...
Ora risulterà anche chiaro che,tutto sommato, la forma polare può essere pensata come una forma sintetica della notazione esponenziale, in cui si mettono in evidenza solamente modulo e argomento: \[\dot{z} = r_z\; e^{i \alpha} \quad \Leftrightarrow \quad r_z\; \angle \alpha \] trovano quindi ulteriore giustificazione le modalità di esecuzione delle operazioni in forma polare nelle analoghe operazioni in forma esponenziale.
2.3 - Potenze e logaritmi complessi
Ci poniamo ora il problema di definire la potenza di base ed esponente complessi e il logaritmo complesso. Detti allora \(\dot{w} = x + i\;y\), \(\dot{s} = a + i\;b\) e \(\dot{z} = c + i\;d\) tre numeri complessi, vorremmo cercare di dare un senso a scritture quali: \(\dot{w}^{\dot{s}} = (x + i\;y)^{(a + i\;b)}\) e \(\dot{w} = ln(\dot{z})\)2.3.1 - La necessità dei logaritmi
Sappiamo bene che, in campo reale, elevare un numero \( a \) alla potenza intera n significa semplicemente moltiplicare \( a \) per se stesso n volte.Non volendo limitarci ai soli esponenti interi, se intendiamo elevare \( a \) alla potenza \( q \), con \( q \) razionale, possiamo ricordare che \( q \) può essere espresso come rapporto di numeri interi m e n, primi fra loro, con n ≠0: \( q = \frac{m}{n} \). Inoltre dovremo porre \( a\; >\; 0 \) per evitare problemi se n è pari. Allora \( a^q = a^{\frac{m}{n}} = (a^m)^{\frac{1}{n}} = \sqrt[n]{a^m} \) e anche in questo caso abbiamo una risposta semplice.
Qualche problema in più si presenta se anche l'esponente è un numero reale irrazionale o trascendente: ad esempio, come possiamo ottenere il valore di \(a^{ \sqrt{2}} = a^{1,41421...} \)?
Questo è principalmente un problema computazionale, la cui difficoltà dipende dal livello di precisione che vogliamo ottenere. Poichè sappiamo calcolare una potenza con esponente razionale possiamo approssimare \(a^{ \sqrt{2}} \approx a^{\frac{14}{10}} = \sqrt[10]{a^{14}} \). Per una maggiore precisione vorremmo sicuramente calcolare \(a^{ \sqrt{2}} \approx a^{\frac{141}{100}} = \sqrt[100]{a^{141}} \) e così via, ma ci rendiamo immediatamente conto di come l'impegno richiesto dal calcolo ( se non si possiedono sofisticati strumenti quali quelli oggi disponibili) possa diventare rapidamente insostenibile. Proprio per tale motivo, agli albori del XVII secolo, quando i calcoli astronomici (nel vero senso della parola) occupavano per settimane e mesi gli scienziati del tempo, sono stati "inventati" i logaritmi.
2.3.2 - I logaritmi
I logaritmi, introdotti dal matematico e fisico scozzese John Napier (Nepero) nel 1614, hanno ricoperto il ruolo di veri e propri strumenti di calcolo anche fino a tempi relativamente recenti (nel 1972 Hewlett-Packard mise sul mercato la prima calcolatrice elettronica tascabile, l' HP-35, con la quale ebbe inizio il progressivo abbandono del regolo calcolatore, che sfruttava appunto le proprietà dei logaritmi). A cosa fu dovuto un così grande e duraturo successo? Essenzialmente al fatto che i logaritmi consentono di trasformare prodotti in somme, potenze in prodotti ed estrazioni di radice in divisioni.
Concettualmente l'importanza del logaritmo va comunque ben oltre la facilitazione nel calcolo che esso può introdurre.
Il logaritmo in base b di un numero x è l'esponente a cui si deve elevare b per ottenere x e quindi se \(x = b^u\), allora \(u = log_b (x)\),
cioè u (l'esponente) è il logaritmo in base b di x e quindi \(x = b^{log_b(x)}\).
Inteso come funzione, il logaritmo è la funzione inversa dell'esponenziale: \(log_b (b^x) = x\)
Le proprietà che rendono i logaritmi un così potente strumento di calcolo sono le seguenti (x e y reali):
| I | \(log_b (x \cdot y) = log_b(x)+log_b(y)\) | trasforma un prodotto in una somma (1) (1' ) |
| II | \(log_b (\frac{x}{y}) = log_b(x)-log_b(y)\) | trasforma un quoziente in una differenza |
| III | \(log_b (x^y) = y\; log_b(x)\) | trasforma una potenza in un prodotto (4) |
| IV | \(log_b (\sqrt[y]{x}) = \frac{1}{y}\; log_b(x)\) | trasforma l'estrazione di radice in una divisione |
Come è noto la base normalmente usata per i logaritmi è il numero di nepero \(e = 2.718281828459...\)
Il logaritmo in base \(e\) viene correntemente indicato con ln ed è chiamato logaritmo naturale: \(ln(x) = log_e(x)\), questo perchè questa base si rivela essere quella più conveniente per il calcolo dei logaritmi.
I logaritmi di Briggs usano la base 10. Essi sono indicati col simbolo log sottintendendo la base, quindi \(log(x) = log_{10}(x)\).
2.3.3 - Il logaritmo complesso
La formula di Eulero ci permette di scrivere qualsiasi numero complesso nella forma:
\[\dot{z} = r_z \; e^{i \alpha+2 k i \pi} \quad \quad k \in \mathbb{Z} \] se, per estensione, applichiamo le definizioni di logaritmo e di esponenziale usate in campo reale e abbiamo: \(\dot{z} = e^{\dot{w}} \) allora \(\dot{w} \) è il logaritmo naturale complesso di \(\dot{z} \):
\[\dot{w} = ln(\dot{z}) = ln(r_z \; e^{i \alpha}) = ln(r_z) + ln(e^{i \alpha}) \] dove si è applicata proprietà I dei logaritmi. Ma \(ln(e^{i \alpha}) = i \alpha \) e quindi:
\[\dot{w} = ln(\dot{z}) = ln(r_z \; e^{i \alpha}) = ln(r_z) + i \alpha \] Osserviamo che la parte immaginaria del logaritmo è costituita proprio dall'argomento α del numero stesso. Ma, come sopra evidenziato nella rappresentazione esponenziale, qualsiasi incremento (o decremento) di multipli di 2π radianti all'argomento rappresenterà lo stesso numero.
Tale ambiguità (per ricordarcene usiamo la notazione \( Ln \) in luogo di \( ln \)) si riflette anche sul logaritmo per cui: \[\dot{w} = Ln(\dot{z}) = ln(r_z) + i Arg(\dot{z}) = ln(r_z) + i (\alpha + 2 k \pi) \quad k \in \mathbb{Z}\] dove \(ln(r_z)\) è chiaramente il logaritmo naturale del numero reale \(r_z\).
Se usiamo nella definizione di logaritmo la determinazione principale dell'argomento α = arg(z) ( −π < α < π )
scriveremo:
\[\dot{w} = ln(\dot{z}) = ln(r_z) + i \; arg(\dot{z}) = ln(r_z) + i \alpha \quad con \quad -\pi < \alpha < \pi \]
Dobbiamo ancora dire qualcosa sull'esponenziale di un numero complesso, supponiamo \(\dot{w} = x + iy \) \[e^\dot{w} = e^{x+iy} = e^x e^{iy} = e^x (cos\; x + i\; sin\; y) \]
Si può dimostrare (5) che ciò equivale a:
\[e^\dot{w} = \lim_{n \to \infty} \left( 1 + \frac{x+ iy}{n}\right)^n = \lim_{n \to \infty} \left( 1 + \frac{\dot{w}}{n}\right)^n \]
2.3.4 - L' elevamento a potenza complessa
Ci poniamo ora il problema di definire la potenza di base ed esponente complessi.
Detti allora \(\dot{w} = x + iy \) e \(\dot{s} = c + id \) due numeri complessi, vorremmo cercare di dare un senso all'operazione: \(\dot{w}^{\dot{s}} = (x + iy)^{c+id} \) Usando per estensione, la proprietà III dei logaritmi, possiamo scrivere:
\[\dot{w}^{\dot{s}} = e^{ln(\dot{w}^{\dot{s}})}= e^{\dot{s}ln(\dot{w})} \]. Tuttavia le operazioni che coinvolgono i logaritmi complessi richiedono molta cautela proprio per la molteplicità dei valori che li caratterizza.
Ad esempio mentre la relazione \(e^{ln(\dot{w})} = \dot{w} = r \angle \beta \) è sempre vera, infatti:
\[e^{ln(\dot{w})} = e^{ln(r)+i\beta} = e^{ln(r)} e^{i\beta} = r e^{i\beta} = \dot{w} \] Così generalmente non accade per \(ln(e^{\dot{w}}) = \dot{w} \) infatti:
\(e^{\dot{w}} = e^x e^{iy} \)
\(ln(e^{\dot{w}}) = ln(e^x e^{iy}) = ln(e^x) + ln(e^{iy})= x + i(y + 2k\pi) \quad k \in \mathbb{Z} \)
Testi dell'autore
Rev. 07/06/2022
(1)
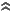 Infatti se
\(u = log_b (x)\; e\; v = log_b(y) \),
allora
\(b^u = x \; e\; b^v = y \).
Infatti se
\(u = log_b (x)\; e\; v = log_b(y) \),
allora
\(b^u = x \; e\; b^v = y \).Poiché \(p = log_b (x \cdot y) \Rightarrow b^p = x \cdot y \), potremo scrivere \(b^p = b^u \cdot b^v \),
ma per le proprietà delle potenze \(p = u+v \), da cui \(log_b (x \cdot y) = log_b(x)+log_b(y)\) (1')
(2)
 Eulero (1707
-1783) pubblicò questa
formula nella
'Introductio Analysin Infinitorum' del 1748, ma essa era nota
a De Moivre (1667-1754) e, in una forma equivalente a
\(ln( cos\; \alpha + i sin\; \alpha)= i \alpha\), anche a Roger Cotes (1682-1716).
Eulero (1707
-1783) pubblicò questa
formula nella
'Introductio Analysin Infinitorum' del 1748, ma essa era nota
a De Moivre (1667-1754) e, in una forma equivalente a
\(ln( cos\; \alpha + i sin\; \alpha)= i \alpha\), anche a Roger Cotes (1682-1716).
(3)
 Il
numero trascendente π
(perchè non è esprimibile mediante una frazione e non è soluzione di
equazioni algebriche) sarebbe una costante universale in uno spazio
'piatto' o spazio euclideo. Come forse è noto la gravitazione comporta
un certo grado di curvatura dello spazio-tempo (Relatività generale di
Einstein, 1916)
dovuto alla presenza delle masse. Questo comporta che su larga scala il
rapporto tra circonferenza e diametro sia diverso da π.
Per comprendere questo fatto si provi a pensare ad una
circonferenza tracciata su una superficie, ad esempio sferica: il
diametro sarebbe in questo caso un arco di circonferenza
massima,
di lunghezza maggiore rispetto al diametro misurato su una superficie
piana. Conseguentemene π avrebbe un valore inferiore a
3.14159...
Il
numero trascendente π
(perchè non è esprimibile mediante una frazione e non è soluzione di
equazioni algebriche) sarebbe una costante universale in uno spazio
'piatto' o spazio euclideo. Come forse è noto la gravitazione comporta
un certo grado di curvatura dello spazio-tempo (Relatività generale di
Einstein, 1916)
dovuto alla presenza delle masse. Questo comporta che su larga scala il
rapporto tra circonferenza e diametro sia diverso da π.
Per comprendere questo fatto si provi a pensare ad una
circonferenza tracciata su una superficie, ad esempio sferica: il
diametro sarebbe in questo caso un arco di circonferenza
massima,
di lunghezza maggiore rispetto al diametro misurato su una superficie
piana. Conseguentemene π avrebbe un valore inferiore a
3.14159...(4)
 se
\(u = log_b (x)\;\; x^a = (b^u)^a = b^{au} = b^{a\;log_b(x)}\) quindi \( log_b(x^a) = a\; log_b(x) \)
se
\(u = log_b (x)\;\; x^a = (b^u)^a = b^{au} = b^{a\;log_b(x)}\) quindi \( log_b(x^a) = a\; log_b(x) \)
(5)
 Per note proprietà dei limiti e degli esponenziali:
\[e^x e^{iy} = \lim_{n \to \infty} \left[ \left( 1 + \frac{x}{n}\right) \left( 1 + \frac{iy}{n}\right)\right]^n \]
Eseguendo il prodotto si ha:
\[\lim_{n \to \infty} \left[ 1 + \frac{x+iy}{n} + \frac{ixy}{n^2}\right]^n \]
Il termine \(\frac{ixy}{n^2}\) va a zero più rapidamente al tendere di n ad
infinito e quindi, in tale situazione può essere trascurato.
Per note proprietà dei limiti e degli esponenziali:
\[e^x e^{iy} = \lim_{n \to \infty} \left[ \left( 1 + \frac{x}{n}\right) \left( 1 + \frac{iy}{n}\right)\right]^n \]
Eseguendo il prodotto si ha:
\[\lim_{n \to \infty} \left[ 1 + \frac{x+iy}{n} + \frac{ixy}{n^2}\right]^n \]
Il termine \(\frac{ixy}{n^2}\) va a zero più rapidamente al tendere di n ad
infinito e quindi, in tale situazione può essere trascurato.