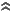Rifasamento degli impianti elettrici

Il rifasamento degli impianti elettrici

1 - La potenza reattiva

La quasi totalità degli utilizzatori elettrici industriali presenta caratteristiche equivalenti a quelle di una impedenza ohmico-induttiva, per la quale la corrente è sfasata in ritardo rispetto alla tensione di un angolo \(\small \varphi_u\)⁽¹⁾. Tale sfasamento indica che vi è, tra generatore e utilizzatore, uno scambio di potenza reattiva. Il funzionamento dei motori elettrici, ad esempio, è determinato dall'interazione di un campo magnetico con le correnti che percorrono i loro circuiti. Per la costruzione del campo magnetico è necessaria l'energia veicolata dalla potenza reattiva, in questo caso induttiva. Come è noto la potenza reattiva non può essere utilizzata per compiere un lavoro all'esterno del sistema elettrico, ma deve essere comunque prodotta dai generatori e messa a disposizione dei dispositivi che ne fanno uso. Essa viene continuamente scambiata tra generatori e utilizzatori e impegna le linee di trasporto con la relativa corrente detta anche corrente reattiva.

Attività 1

2 - Corrente attiva e corrente reattiva

La corrente assorbita dall'utilizzatore può essere scomposta in due componenti:
la corrente attiva, in fase con la tensione, data da:

\[I_a = I_u\,cos\,\varphi_u \]
e la già nominata corrente reattiva, in quadratura con la tensione:

\[I_r = I_u\,sin\,\varphi_u \]

Naturalmente, fissata la tensione di alimentazione V, la componente attiva è proporzionale alla potenza attiva:

\[P_u = V\,I_u\,cos\,\varphi_u = V\,I_a \]

mentre la componente reattiva è proporzionale alla potenza reattiva:

\[Q_u = V\,I_u\,sin\,\varphi_u = V\,I_r \]
La rete di alimentazione e i generatori devono fornire all'utilizzatore sia la potenza attiva che verrà utilizzata per produrre lavoro, sia la potenza reattiva necessaria.
Tuttavia è noto che induttore e condensatore, dal punto di vista della potenza reattiva, hanno comportamenti complementari, nel senso che, alimentati da una stessa tensione alternata sinusoidale, il condensatore eroga potenza reattiva quando l'induttore la assorbe e viceversa.

3 - Rifasamento

Quanto sopra suggerisce che lo scambio di energia reattiva, che normalmente avviene tra utilizzatore e generatore, possa invece avvenire tra un utilizzatore ohmico-induttivo e un condensatore collegato in parallelo all'utilizzatore stesso.
Il collegamento in parallelo ovviamente, ha lo scopo di non alterare la tensione sul carico (simulato dall'impedenza R-L) e quindi la modalità di funzionamento del carico stesso.
Se inseriamo il condensatore osserviamo immediatamente che viene ridotto l'angolo di sfasamento e contemporaneamente il modulo della corrente diminuisce.
Analizzando meglio la situazione, noteremo anche che la corrente assorbita dall'utilizzatore \(I_u\) è rimasta invariata.
La corrente del ramo capacitivo, in quadratura in anticipo sulla tensione, sommata alla corrente \(I_u\) dà come risultato la corrente totale di linea \(I_T\).
L'angolo di sfasamento φ_u è a sua volta rimasto invariato, il che conferma che l'utilizzatore funziona esattamente come avveniva prima dell'inserimento del condensatore, assorbendo la stessa corrente, la stessa potenza attiva e la stessa potenza reattiva.
La potenza reattiva che impegna la linea è invece diminuita, poiché parte dello scambio di energia avviene direttamente tra induttore e condensatore. Infatti la componente reattiva della corrente totale è diminuita.
La componente attiva della corrente rimane costante e ciò ribadisce il fatto che non varia la potenza attiva assorbita. D'altra parte il condensatore assorbe solo potenza reattiva e quindi non può modificare la situazione in tal senso.
Tracciando anche la componente reattiva \(\small I_{ur}\) della corrente assorbita dall'utilizzatore si possono scrivere alcune relazioni importanti. Per esempio:

\[I_a = I_T\,cos\,\varphi = I_u\,cos\,\varphi_u\]
che afferma l'uguaglianza delle componenti attive sia della corrente totale \(I_T\) che della corrente sull'utilizzatore \(I_u\).
La componente reattiva della corrente totale può essere determinata a partire dalla componente attiva:

\[I_r = I_T\,sin\,\varphi = I_a\,tan\,\varphi\]

e questo vale anche per la componente reattiva della corrente sull'utilizzatore \(I_{ur}\):

\[I_{ur} = I_u\,sin\,\varphi = I_a\,tan\,\varphi_u\]

Dal diagramma vettoriale dei fasori si osserva che la corrente sul condensatore può essere vista come differenza delle due componenti reattive:

\[I_c = I_{ur} - I_r\]
Applicando le formule precedenti:

\[I_c = I_a\,(tan\,\varphi_u - tan\,\varphi)\]
Moltiplicando entrambe i membri di quest'ultima relazione per V si ha:

\[V\,I_c = V\,I_a\,(tan\,\varphi_u - tan\,\varphi)\]
e quindi:

\[V\,I_c = V\,I_u\,cos\,\varphi_u\,(tan\,\varphi_u - tan\,\varphi)\]
Poiché \(V\,I_c = Q_c \) è la potenza reattiva assorbita dal condensatore, mentre chiaramente \(V\,I_u\,cos\,\varphi_u \) è la potenza attiva assorbita dall'utilizzatore:

\[Q_c = P_u\,(tan\,\varphi_u - tan\,\varphi)\]
Quest'ultima è anche detta potenza reattiva rifasante.
Poiché vale la relazione:

\[Q_c = \frac{V^2}{X_c} = \frac{V^2}{\frac{1}{\omega C}} = \omega\,C\,V^2\]
si può determinare la capacità rifasante:

\[C = \frac{P_u}{\omega V^2}\,(tan\,\varphi_u - tan\,\varphi)\]

Attività 2: Problema

Un utilizzatore assorbe a 230 V, 50 Hz, una potenza attiva di 5 kW e reattiva induttiva di 8 kVAR ed è alimentato da una linea di impedenza 0,2 + j 0,3 Ω. Si vuole rifasare l'utilizzatore a cosfì 0,9 mantendo a 230 V la tensione di arrivo della linea. Determinare la capacità da inserire in parallelo, la corrente sul carico dopo il rifasamento, la corrente totale di linea, la cdt in linea in percentuale sulla tensione di arrivo.

Determiniamo la potenza apparente:

\[S = \sqrt{P^2 + Q^2} = \sqrt{5^2 + 8^2} = 9,43 \;\;kVA\]

da cui ricaviamo la corrente assorbita:

\[I = \frac{S}{V} = \frac{9430}{230} = 41\;\;A \]
e il fattore di potenza:

\[cos\,\varphi_u = \frac{P}{S} = \frac{5}{9,43} = 0,530\]
\[\varphi_u = arccos\,0,530 = 58° \]
Considerando nulla la fase della tensione:

\[V = 230\, \angle 0°\;\;V \]
la corrente avrà fase -58° e, in forma polare:

\[I = 41\, \angle -58°\;\;A \]
Sulla linea di alimentazione vengono dissipati:

\[P_l = R_l\,I^2 = 0,2 \cdot 41^2 = 336\;\;W\]

La tensione alla partenza della linea può essere determinata con la formula approssimata della cdt indutriale:

\[V_0 = V + I ( R_l\, cos\, \varphi_u + X_l\,sin\,\varphi_u) \]
quindi:

\[V_0 = 230 + 41\,( 0,2 \cdot 0,530 + 0,3 \cdot 0,848) = 245\;\;V \]
Possiamo ora determinare la capacità rifasante per avere un fattore di potenza pari a 0,9, cui corrisponde:

\[\varphi = arccos\,0,9 = 25,8° \qquad tan\,\varphi = 0,484\]
e quindi:

\[C = \frac{P}{\omega V^2}(tan\, \varphi_u - tan\, \varphi)\]

e quindi:
\[C = \frac{5000}{314 \cdot 230^2}(1,6 - 0,484) = 336\;\;\mu F\]

dopo il rifasamento avremo in linea una corrente:
\[I = \frac{P}{V\,cos\, \varphi} = \frac{5000}{230 \cdot 0,9} = 24\;\;A\]
In forma polare:

\[I = 24\, \angle -25,8°\;\;A \]
Perdite in linea pari a:

\[P_l = R_l\,I^2 = 0,2 \cdot 24^2 = 115\;\;W\]

e una tensione in partenza della linea di:

\[V_0 = 230 + 24\,( 0,2 \cdot 0,9 + 0,3 \cdot 0,436) = 237,5\;\;V \]

Verifica sulla lavagna a sinistra i valori delle correnti e del cosfì. Per fare questo dovrai impostare opportunamente i parametri del circuito, eseguendo qualche calcolo. Prosegui secondo lo schema seguente rispondendo alle domande (usa il punto decimale in luogo della virgola). Se la risposta è corretta verrà impostato il giusto valore:

chiudi

Teoricamente sarebbe possibile rifasare completamente il carico, portando la corrente totale ad essere in fase con la tensione. In tal caso, essendo \(\varphi = 0\) e \(tan\,\varphi = 0\) , si avrebbe:

\[C = \frac{P\,tan\,\varphi_u}{\omega\,V^2} = \frac{Q_u}{\omega\, V^2}\]
ma questa non è una situazione normalmente perseguita dovendosi assolutamente evitare la possibilità che un "eccesso di rifasamento", che potrebbe verificarsi al variare delle condizioni di funzionamento, renda globalmente ohmico-capacitivo il carattere del carico. Non si desidera avere carichi capacitivi a causa delle sovratensioni che questi possono generare all'arrivo della linea di alimentazione (effetto Ferranti, fig.1)

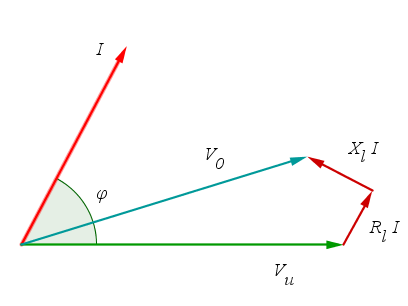
Fig.1 - L'effetto Ferranti. Con carichi fortemente capacitivi la tensione di arrivo \(\small V_u\) della linea può superare il valore della tensione in partenza \(\small V_0\).

4 - Triangolo delle potenze

L'effetto del rifasamento risulta molto evidente se si prende in considerazione il triangolo delle potenze. Si osserva che inserendo il condensatore la potenza attiva resta invariata mentre potenza reattiva e apparente totali diminuiscono, anche se la potenza reattiva assorbita dal carico non cambia.
Come già detto si deve evitare di immettere in rete potenza reativa capacitiva e quindi prudenzialmente si rifasa ad un valore del cosfì inferiore all'unità.
L'ente di distribuzione dell'energia elettrica pone il valore 0,9 come riferimento.
Impianti con fattore di potenza inferiore vengono penalizzati con una maggior costo dell'energia. Se il fattore di potenza è inferiore o uguale a 0,7 vi è comunque l'obbligo di rifasare.

5 - Valori nominali della batteria di condensatori

Una batteria di condensatori di capacità C fornisce la potenza reattiva nominale quando è sottoposta alla tensione nominale:

\[Q_{Cn} = \frac{V_n^2}{X_C} = \omega\,C\,V_n^2 \]
che dipende chiaramente dal quadrato della tensione.
Dovendo utilizzare la batteria ad una tensione diversa da quella nominale, a parità di frequenza, si avrà una potenza rifasante:

\[ Q_C = \omega\, C\, V^2 = Q_{Cn}\,\frac{V^2}{V_n^2}\]

Essendo poi:

\[I_C = \frac{V}{X_C} = \omega\,C\,V\]
si ha per la corrente nominale:

\[I_{Cn} = \omega\,C\,V_n \]
e quindi:

\[I_C = I_{Cn}\, \frac{V}{V_n}\]

6 - Rifasamento trifase

Nel rifasamento di un sistema trifase, la capacità rifasante è anche funzione del tipo di collegamento tra i condensatori che si intende realizzare.
Nel caso di rifasamento mediante batterie di condensatori collegate a stella, detta V la tensione concatenata o di linea ed E la tensione di fase, si ha:

\[C_Y = \frac{P}{3\,\omega\, E^2}\,(tan\,\varphi_u - tan\,\varphi)\]

e poiché: \(\small E = \dfrac{V}{\sqrt{3}}\), sostituendo nella precedente:

\[C_Y = \frac{P}{3\,\omega\, \left(\frac{V}{\sqrt{3}} \right)^2}\,(tan\,\varphi_u - tan\,\varphi) = \frac{P}{\omega\, V^2}\,(tan\,\varphi_u - tan\,\varphi)\]

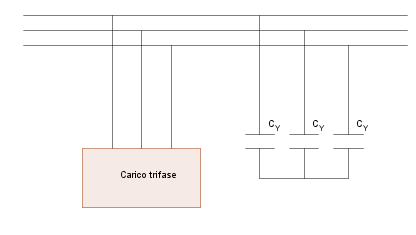
Fig. 2 - Rifasamento trifase mediante condensatori collegati a stella

Nel collegamento a triangolo, essendo V anche tensione di fase:

\[C_D = \frac{P}{3\,\omega\, V^2}\,(tan\,\varphi_u - tan\,\varphi)\]

La conclusione è che con questo tipo di collegamento si ottengono gli stessi effetti utilizzando però condensatori con capacità pari a 1/3 di quella necessaria con il collegamento a stella:

\[C_D = \frac{C_Y}{3}\]
Per tale ragione, a bassa tensione, il rifasamento avviene sempre collegando a triangolo le batterie di condensatori.
A tensioni medio-alte può convenire il rifasamento a stella per questioni di isolamento dato che, in tal caso, i condensatori possono essere dimensionati per una tensione \(\sqrt{3}\) volte inferiore.

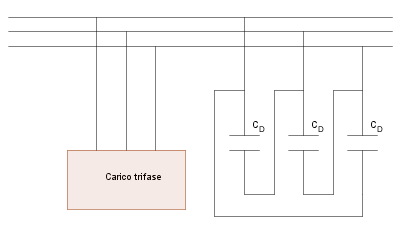
Fig. 3 - Rifasamento trifase con collegamento a triangolo

7 - Vantaggi del rifasamento e prescrizioni

Riassumendo, i vantaggi di un corretto rifasamento sono:

diminuzione della corrente di linea a parità di altre condizioni di funzionamednto degli utilizzatori elettrici; possibilità quindi di ridurre le sezioni dei conduttori o di alimentare un maggior numero di utilizzatori con la stessa linea
diminuzione delle perdite in linea che sono proporzionali al quadrato della corrente
dimuinuzione delle cadute di tensione in linea

Prescrizioni per impianti con potenza impegnata superiore a 16,5 kW:

il fattore di potenza medio mensile non può essere inferiore a 0,7
il livello minimo del fattore di potenza istantaneo in corrispondenza del massimo carico per prelievi nei periodi di alto carico è pari a 0,9
con 0,7 < cos φ < 0,95 l'energia nelle fasce orarie F1 e F2 è gravata da sovrapprezzo
divieto assoluto di immettere potenza reattiva (capacitiva) in rete (eccesso di rifasamento)

Per la normativa si può vedere il sito dell'Autorità di Regolazione per Energia Reti e Ambiente, in particolare la delibera180/2013/R/eel.

8 - Argomenti correlati e approfondimenti

⁽¹⁾ Con l'indice 'u' intendiamo riferirci alle grandezze proprie dell'utilizzatore, in questo caso simulato da un'impedenza ohmico-induttiva. Ricordiamo che con il termine 'utilizzatore' si intende qualsiasi dispositivo che assorba potenza elettrica e che alcune volte viene anche indicato come 'carico' (sottinteso: elettrico).